
Oscillations in linear systems
 المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
 المصدر:
The Feynman Lectures on Physics
المصدر:
The Feynman Lectures on Physics
 الجزء والصفحة:
Volume I, Chapter 25
الجزء والصفحة:
Volume I, Chapter 25
 2024-03-14
2024-03-14
 1644
1644
Let us now review the things we have been talking about in the past few chapters. It is very easy for the physics of oscillators to become obscured by the mathematics. The physics is actually very simple, and if we may forget the mathematics for a moment, we shall see that we can understand almost everything that happens in an oscillating system. First, if we have only the spring and the weight, it is easy to understand why the system oscillates—it is a consequence of inertia. We pull the mass down and the force pulls it back up; as it passes zero, which is the place it likes to be, it cannot just suddenly stop; because of its momentum it keeps on going and swings to the other side, and back and forth. So, if there were no friction, we would surely expect an oscillatory motion, and indeed we get one. But if there is even a little bit of friction, then on the return cycle, the swing will not be quite as high as it was the first time.
Now what happens, cycle by cycle? That depends on the kind and amount of friction. Suppose that we could concoct a kind of friction force that always remains in the same proportion to the other forces, of inertia and in the spring, as the amplitude of oscillation varies. In other words, for smaller oscillations the friction should be weaker than for big oscillations. Ordinary friction does not have this property, so a special kind of friction must be carefully invented for the very purpose of creating a friction that is directly proportional to the velocity—so that for big oscillations it is stronger and for small oscillations it is weaker. If we happen to have that kind of friction, then at the end of each successive cycle the system is in the same condition as it was at the start, except a little bit smaller. All the forces are smaller in the same proportion: the spring force is reduced, the inertial effects are lower because the accelerations are now weaker, and the friction is less too, by our careful design. When we actually have that kind of friction, we find that each oscillation is exactly the same as the first one, except reduced in amplitude. If the first cycle dropped the amplitude, say, to 90 percent of what it was at the start, the next will drop it to 90 percent of 90 percent, and so on: the sizes of the oscillations are reduced by the same fraction of themselves in every cycle. An exponential function is a curve which does just that. It changes by the same factor in each equal interval of time. That is to say, if the amplitude of one cycle, relative to the preceding one, is called a, then the amplitude of the next is a2, and of the next, a3. So the amplitude is some constant raised to a power equal to the number of cycles traversed:

But of course, n∝t, so it is perfectly clear that the general solution will be some kind of an oscillation, sine or cosine ωt, times an amplitude which goes as bt more or less. But b can be written as e−c, if b is positive and less than 1. So this is why the solution looks like e−ct cos ω0t. It is very simple.
What happens if the friction is not so artificial; for example, ordinary rubbing on a table, so that the friction force is a certain constant amount, and is independent of the size of the oscillation that reverses its direction each half-cycle? Then the equation is no longer linear, it becomes hard to solve, and must be solved by the numerical method, or by considering each half-cycle separately. The numerical method is the most powerful method of all, and can solve any equation. It is only when we have a simple problem that we can use mathematical analysis.
Mathematical analysis is not the grand thing it is said to be; it solves only the simplest possible equations. As soon as the equations get a little more complicated, just a shade—they cannot be solved analytically. But the numerical method, which was advertised at the beginning of the course, can take care of any equation of physical interest.
Next, what about the resonance curve? Why is there a resonance? First, imagine for a moment that there is no friction, and we have something which could oscillate by itself. If we tapped the pendulum just right each time it went by, of course we could make it go like mad. But if we close our eyes and do not watch it, and tap at arbitrary equal intervals, what is going to happen? Sometimes we will find ourselves tapping when it is going the wrong way. When we happen to have the timing just right, of course, each tap is given at just the right time, and so it goes higher and higher and higher. So without friction we get a curve which looks like the solid curve in Fig. 25–5 for different frequencies. Qualitatively, we understand the resonance curve; in order to get the exact shape of the curve it is probably just as well to do the mathematics. The curve goes toward infinity as ω→ω0, where ω0 is the natural frequency of the oscillator.
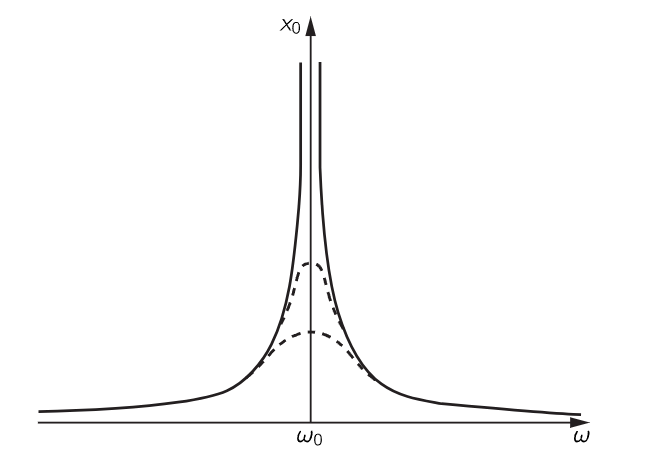
Fig. 25–5. Resonance curves with various amounts of friction present.
Now suppose there is a little bit of friction; then when the displacement of the oscillator is small, the friction does not affect it much; the resonance curve is the same, except when we are near resonance. Instead of becoming infinite near resonance, the curve is only going to get so high that the work done by our tapping each time is enough to compensate for the loss of energy by friction during the cycle. So the top of the curve is rounded off—it does not go to infinity. If there is more friction, the top of the curve is rounded off still more. Now someone might say, “I thought the widths of the curves depended on the friction.” That is because the curve is usually plotted so that the top of the curve is called one unit. However, the mathematical expression is even simpler to understand if we just plot all the curves on the same scale; then all that happens is that the friction cuts down the top! If there is less friction, we can go farther up into that little pinnacle before the friction cuts it off, so it looks relatively narrow. That is, the higher the peak of the curve, the narrower the width at half the maximum height.
Finally, we take the case where there is an enormous amount of friction. It turns out that if there is too much friction, the system does not oscillate at all. The energy in the spring is barely able to move it against the frictional force, and so it slowly oozes down to the equilibrium point.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


