We shall discuss the forced harmonic oscillator, i.e., one in which there is an external driving force acting. The equation then is the following:

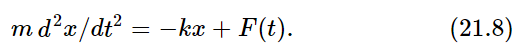
We would like to find out what happens in these circumstances. The external driving force can have various kinds of functional dependence on the time; the first one that we shall analyze is very simple—we shall suppose that the force is oscillating:

Notice, however, that this ω is not necessarily ω₀: we have ω under our control; the forcing may be done at different frequencies. So, we try to solve Eq. (21.8) with the special force (21.9). What is the solution of (21.8)? One special solution, (we shall discuss the more general cases later) is

where the constant is to be determined. In other words, we might suppose that if we kept pushing back and forth, the mass would follow back and forth in step with the force. We can try it anyway. So we put (21.10) and (21.9) into (21.8), and get

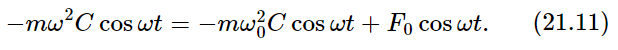
We have also put in k=mω²₀, so that we will understand the equation better at the end. Now because the cosine appears everywhere, we can divide it out, and that shows that (21.10) is, in fact, a solution, provided we pick C just right. The answer is that C must be

That is, m oscillates at the same frequency as the force, but with an amplitude which depends on the frequency of the force, and also upon the frequency of the natural motion of the oscillator. It means, first, that if ω is very small compared with ω₀, then the displacement and the force are in the same direction. On the other hand, if we shake it back and forth very fast, then (21.12) tells us that C is negative if ω is above the natural frequency ω₀ of the harmonic oscillator. (We will call ω₀ the natural frequency of the harmonic oscillator, and ω the applied frequency.) At very high frequency the denominator may become very large, and there is then not much amplitude.

Of course, the solution we have found is the solution only if things are started just right, for otherwise there is a part which usually dies out after a while. This other part is called the transient response to F(t), while (21.10) and (21.12) are called the steady-state response.

According to our formula (21.12), a very remarkable thing should also occur: if ω is almost exactly the same as ω₀, then C should approach infinity. So, if we adjust the frequency of the force to be “in time” with the natural frequency, then we should get an enormous displacement. This is well known to anybody who has pushed a child on a swing. It does not work very well to close our eyes and push at a certain speed at random. If we happen to get the right timing, then the swing goes very high, but if we have the wrong timing, then sometimes we may be pushing when we should be pulling, and so on, and it does not work.

If we make ω exactly equal to ω₀, we find that it should oscillate at an infinite amplitude, which is, of course, impossible. The reason it does not is that something goes wrong with the equation, there are some other frictional terms, and other forces, which are not in (21.8) but which occur in the real world. So, the amplitude does not reach infinity for some reason; it may be that the spring breaks!