
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Scalar product of vectors
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 11
2024-02-11
1645
Now let us examine a little further the properties of vectors. It is easy to see that the length of a step–in space would be the same in any coordinate system. That is, if a particular step r is represented by x,y,z, in one coordinate system, and by x′,y′,z′ in another coordinate system, surely the distance r=|r| would be the same in both. Now
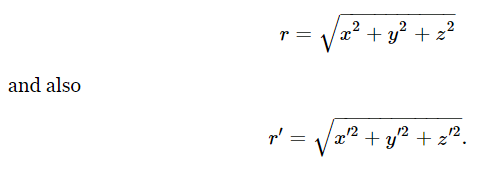
So, what we wish to verify is that these two quantities are equal. It is much more convenient not to bother to take the square root, so let us talk about the square of the distance; that is, let us find out whether
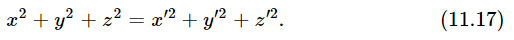
It had better be—and if we substitute Eq. (11.5) we do indeed find that it is. So, we see that there are other kinds of equations which are true for any two coordinate systems.
Something new is involved. We can produce a new quantity, a function of x, y, and z, called a scalar function, a quantity which has no direction but which is the same in both systems. Out of a vector we can make a scalar. We have to find a general rule for that. It is clear what the rule is for the case just considered: add the squares of the components. Let us now define a new thing, which we call a⋅ a. This is not a vector, but a scalar; it is a number that is the same in all coordinate systems, and it is defined to be the sum of the squares of the three components of the vector:

Now you say, “But with what axes?” It does not depend on the axes; the answer is the same in every set of axes. So, we have a new kind of quantity, a new invariant or scalar produced by one vector “squared.” If we now define the following quantity for any two vectors a and b:
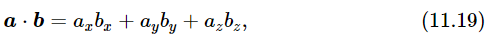
we find that this quantity, calculated in the primed and unprimed systems, also stays the same. To prove it we note that it is true of a⋅ a, b⋅ b, and c⋅ c, where c=a+b. Therefore, the sum of the squares (ax+bx)2+(ay+by)2+(az+bz)2 will be invariant:
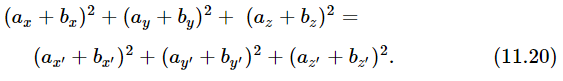
If both sides of this equation are expanded, there will be cross products of just the type appearing in Eq. (11.19), as well as the sums of squares of the components of a and b. The invariance of terms of the form of Eq. (11.18) then leaves the cross product terms (11.19) invariant also.
The quantity a⋅ b is called the scalar product of two vectors, a and b, and it has many interesting and useful properties. For instance, it is easily proved that

Also, there is a simple geometrical way to calculate a⋅ b, ithout having to calculate the components of a and b: a⋅ b is the product of the length of a and the length of b times the cosine of the angle between them. Why? Suppose that we choose a special coordinate system in which the x–axis lies along a; in those circumstances, the only component of a that will be there is ax, which is of course the whole length of a. Thus Eq. (11.19) reduces to a⋅b=axbx for this case, and this is the length of a times the component of b in the direction of a, that is, b cos θ:
a⋅b=ab cos θ.
Therefore, in that special coordinate system, we have proved that a⋅ b is the length of a times the length of b times cos θ. But if it is true in one coordinate system, it is true in all, because a⋅ b is independent of the coordinate system; that is our argument.
What good is the dot product? Are there any cases in physics where we need it? Yes, we need it all the time. For instance, in Chapter 4 the kinetic energy was called 1/2 mv2, but if the object is moving in space it should be the velocity squared in the x–direction, the y–direction, and the z–direction, and so the formula for kinetic energy according to vector analysis is
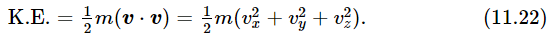
Energy does not have direction. Momentum has direction; it is a vector, and it is the mass times the velocity vector.
Another example of a dot product is the work done by a force when something is pushed from one place to the other. We have not yet defined work, but it is equivalent to the energy change, the weights lifted, when a force F acts through a distance s:

It is sometimes very convenient to talk about the component of a vector in a certain direction (say the vertical direction because that is the direction of gravity). For such purposes, it is useful to invent what we call a unit vector in the direction that we want to study. By a unit vector we mean one whose dot product with itself is equal to unity. Let us call this unit vector i; then i⋅i=1. Then, if we want the component of some vector in the direction of i, we see that the dot product a⋅i will be a cos θ, i.e., the component of a in the direction of i. This is a nice way to get the component; in fact, it permits us to get all the components and to write a rather amusing formula. Suppose that in a given system of coordinates, x, y, and z, we invent three vectors: i, a unit vector in the direction x; j, a unit vector in the direction y; and k, a unit vector in the direction z. Note first that i⋅i=1. What is i⋅j? When two vectors are at right angles, their dot product is zero. Thus
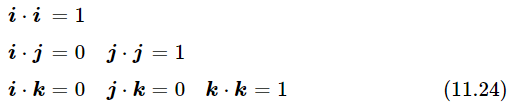
Now with these definitions, any vector whatsoever can be written this way:

By this means we can go from the components of a vector to the vector itself.
This discussion of vectors is by no means complete. However, rather than try to go more deeply into the subject now, we shall first learn to use in physical situations some of the ideas so far discussed. Then, when we have properly mastered this basic material, we shall find it easier to penetrate more deeply into the subject without getting too confused. We shall later find that it is useful to define another kind of product of two vectors, called the vector product, and written as a×b.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















