
Rotations
 المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
 المصدر:
The Feynman Lectures on Physics
المصدر:
The Feynman Lectures on Physics
 الجزء والصفحة:
Volume I, Chapter 11
الجزء والصفحة:
Volume I, Chapter 11
 2024-02-10
2024-02-10
 1402
1402
The next proposition is that it should make no difference in which direction we choose the axes. In other words, if we build a piece of equipment in some place and watch it operate, and nearby we build the same kind of apparatus but put it up on an angle, will it operate in the same way? Obviously, it will not if it is a Grandfather clock, for example! If a pendulum clock stands upright, it works fine, but if it is tilted the pendulum falls against the side of the case and nothing happens. The theorem is then false in the case of the pendulum clock, unless we include the earth, which is pulling on the pendulum. Therefore, we can make a prediction about pendulum clocks if we believe in the symmetry of physical law for rotation: something else is involved in the operation of a pendulum clock besides the machinery of the clock, something outside it that we should look for. We may also predict that pendulum clocks will not work the same way when located in different places relative to this mysterious source of asymmetry, perhaps the earth. Indeed, we know that a pendulum clock up in an artificial satellite, for example, would not tick either, because there is no effective force, and on Mars it would go at a different rate. Pendulum clocks do involve something more than just the machinery inside, they involve something on the outside. Once we recognize this factor, we see that we must turn the earth along with the apparatus. Of course, we do not have to worry about that, it is easy to do; one simply waits a moment or two and the earth turns; then the pendulum clock ticks again in the new position the same as it did before. While we are rotating in space our angles are always changing, absolutely; this change does not seem to bother us very much, for in the new position we seem to be in the same condition as in the old. This has a certain tendency to confuse one, because it is true that in the new turned position the laws are the same as in the unturned position, but it is not true that as we turn a thing it follows the same laws as it does when we are not turning it. If we perform sufficiently delicate experiments, we can tell that the earth is rotating, but not that it had rotated. In other words, we cannot locate its angular position, but we can tell that it is changing.
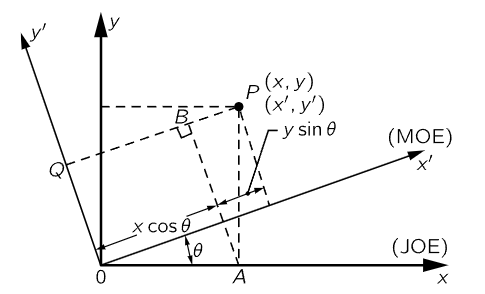
Fig. 11–2. Two coordinate systems having different angular orientations.
Now we may discuss the effects of angular orientation upon physical laws. Let us find out whether the same game with Joe and Moe works again. This time, to avoid needless complication, we shall suppose that Joe and Moe use the same origin (we have already shown that the axes can be moved by translation to another place). Assume that Moe’s axes have rotated relative to Joe’s by an angle θ. The two coordinate systems are shown in Fig. 11–2, which is restricted to two dimensions. Consider any point P having coordinates (x,y) in Joe’s system and (x′,y′) in Moe’s system. We shall begin, as in the previous case, by expressing the coordinates x′ and y′ in terms of x, y, and θ. To do so, we first drop perpendiculars from P to all four axes and draw AB perpendicular to PQ. Inspection of the figure shows that x′ can be written as the sum of two lengths along the x′–axis, and y′ as the difference of two lengths along AB. All these lengths are expressed in terms of x, y, and θ in equations (11.5), to which we have added an equation for the third dimension.
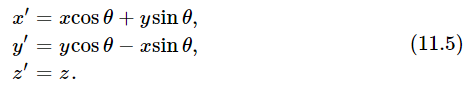
The next step is to analyze the relationship of forces as seen by the two observers, following the same general method as before. Let us assume that a force F, which has already been analyzed as having components Fx and Fy (as seen by Joe), is acting on a particle of mass m, located at point P in Fig. 11–2. For simplicity, let us move both sets of axes so that the origin is at P, as shown in Fig. 11–3. Moe sees the components of F along his axes as Fx′ and Fy′. Fx has components along both the x′– and y′–axes, and Fy likewise has components along both these axes. To express Fx′ in terms of Fx and Fy, we sum these components along the x′–axis, and in a like manner we can express Fy′ in terms of Fx and Fy. The results are
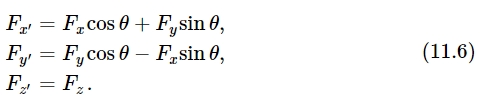
It is interesting to note an accident of sorts, which is of extreme importance: the formulas (11.5) and (11.6), for coordinates of P and components of F, respectively, are of identical form.

Fig. 11–3. Components of a force in the two systems.
As before, Newton’s laws are assumed to be true in Joe’s system, and are expressed by equations (11.1). The question, again, is whether Moe can apply Newton’s laws—will the results be correct for his system of rotated axes? In other words, if we assume that Eqs. (11.5) and (11.6) give the relationship of the measurements, is it true or not true that
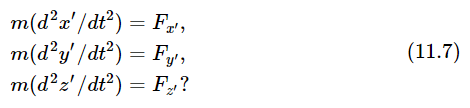
To test these equations, we calculate the left and right sides independently, and compare the results. To calculate the left sides, we multiply equations (11.5) by m, and differentiate twice with respect to time, assuming the angle θ to be constant. This gives
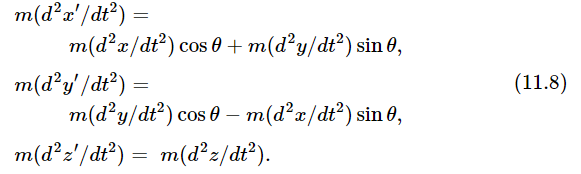
We calculate the right sides of equations (11.7) by substituting equations (11.1) into equations (11.6). This gives

Behold! The right sides of Eqs. (11.8) and (11.9) are identical, so we conclude that if Newton’s laws are correct on one set of axes, they are also valid on any other set of axes. This result, which has now been established for both translation and rotation of axes, has certain consequences: first, no one can claim his particular axes are unique, but of course they can be more convenient for certain particular problems. For example, it is handy to have gravity along one axis, but this is not physically necessary. Second, it means that any piece of equipment which is completely self–contained, with all the force–generating equipment completely inside the apparatus, would work the same when turned at an angle.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


