
Description of motion
 المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
 المصدر:
The Feynman Lectures on Physics
المصدر:
The Feynman Lectures on Physics
 الجزء والصفحة:
Volume I, Chapter 8
الجزء والصفحة:
Volume I, Chapter 8
 2024-02-04
2024-02-04
 1496
1496
In order to find the laws governing the various changes that take place in bodies as time goes on, we must be able to describe the changes and have some way to record them. The simplest change to observe in a body is the apparent change in its position with time, which we call motion. Let us consider some solid object with a permanent mark, which we shall call a point, that we can observe. We shall discuss the motion of the little marker, which might be the radiator cap of an automobile or the center of a falling ball, and shall try to describe the fact that it moves and how it moves.
These examples may sound trivial, but many subtleties enter into the description of change. Some changes are more difficult to describe than the motion of a point on a solid object, for example the speed of drift of a cloud that is drifting very slowly, but rapidly forming or evaporating, or the change of a woman’s mind. We do not know a simple way to analyze a change of mind, but since the cloud can be represented or described by many molecules, perhaps we can describe the motion of the cloud in principle by describing the motion of all its individual molecules. Likewise, perhaps even the changes in the mind may have a parallel in changes of the atoms inside the brain, but we have no such knowledge yet.
At any rate, that is why we begin with the motion of points; perhaps we should think of them as atoms, but it is probably better to be rougher in the beginning and simply to think of some kind of small objects—small, that is, compared with the distance moved. For instance, in describing the motion of a car that is going a hundred miles, we do not have to distinguish between the front and the back of the car. To be sure, there are slight differences, but for rough purposes we say “the car,” and likewise it does not matter that our points are not absolute points; for our present purposes it is not necessary to be extremely precise. Also, while we take a first look at this subject, we are going to forget about the three dimensions of the world. We shall just concentrate on moving in one direction, as in a car on one road. We shall return to three dimensions after we see how to describe motion in one dimension. Now, you may say, “This is all some kind of trivia,” and indeed it is. How can we describe such a one-dimensional motion—let us say, of a car? Nothing could be simpler. Among many possible ways, one would be the following. To determine the position of the car at different times, we measure its distance from the starting point and record all the observations. In Table 8–1, s represents the distance of the car, in feet, from the starting point, and t represents the time in minutes. The first line in the table represents zero distance and zero time—the car has not started yet. After one minute it has started and has gone 1200 feet. Then in two minutes, it goes farther—notice that it picked up more distance in the second minute—it has accelerated; but something happened between 3 and 4 and even more so at 5—it stopped at a light perhaps? Then it speeds up again and goes 13,000 feet by the end of 6 minutes, 18,000 feet at the end of 7 minutes, and 23,500 feet in 8 minutes; at 9 minutes it has advanced to only 24,000 feet, because in the last minute it was stopped by a cop.
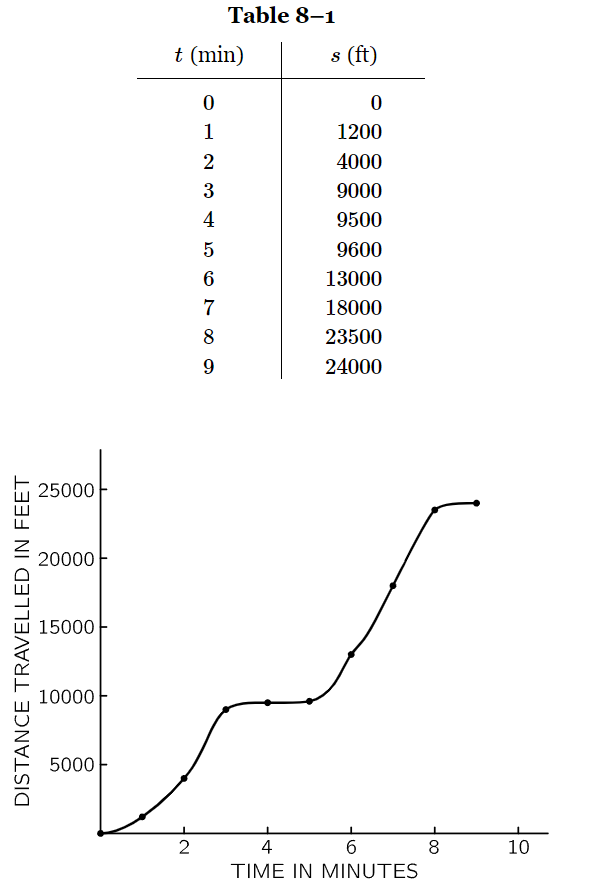
Fig. 8–1. Graph of distance versus time for the car.
That is one way to describe the motion. Another way is by means of a graph. If we plot the time horizontally and the distance vertically, we obtain a curve something like that shown in Fig. 8–1. As the time increases, the distance increases, at first very slowly and then more rapidly, and very slowly again for a little while at 4 minutes; then it increases again for a few minutes and finally, at 9 minutes, appears to have stopped increasing. These observations can be made from the graph, without a table. Obviously, for a complete description one would have to know where the car is at the half-minute marks, too, but we suppose that the graph means something, that the car has some position at all the intermediate times.

Fig. 8–2. Graph of distance versus time for a falling body.
The motion of a car is complicated. For another example, we take something that moves in a simpler manner, following more simple laws: a falling ball. Table 8–2 gives the time in seconds and the distance in feet for a falling body. At zero seconds the ball starts out at zero feet, and at the end of 1 second it has fallen 16 feet. At the end of 2 seconds, it has fallen 64 feet, at the end of 3 seconds, 144 feet, and so on; if the tabulated numbers are plotted, we get the nice parabolic curve shown in Fig. 8–2. The formula for this curve can be written as

This formula enables us to calculate the distances at any time. You might say there ought to be a formula for the first graph too. Actually, one may write such a formula abstractly, as

meaning that s is some quantity depending on t or, in mathematical phraseology, s is a function of t. Since we do not know what the function is, there is no way we can write it in definite algebraic form.
We have now seen two examples of motion, adequately described with very simple ideas, no subtleties. However, there are subtleties—several of them. In the first place, what do we mean by time and space? It turns out that these deep philosophical questions have to be analyzed very carefully in physics, and this is not so easy to do. The theory of relativity shows that our ideas of space and time are not as simple as one might think at first sight. However, for our present purposes, for the accuracy that we need at first, we need not be very careful about defining things precisely. Perhaps you say, “That’s a terrible thing—I learned that in science we have to define everything precisely.” We cannot define anything precisely! If we attempt to, we get into that paralysis of thought that comes to philosophers, who sit opposite each other, one saying to the other, “You don’t know what you are talking about!” The second one says, “What do you mean by know? What do you mean by talking? What do you mean by you?” and so on. In order to be able to talk constructively, we just have to agree that we are talking about roughly the same thing. You know as much about time as we need for the present, but remember that there are some subtleties that have to be discussed; we shall discuss them later.
Another subtlety involved, and already mentioned, is that it should be possible to imagine that the moving point we are observing is always located somewhere. (Of course, when we are looking at it, there it is, but maybe when we look away it isn’t there.) It turns out that in the motion of atoms, that idea also is false—we cannot find a marker on an atom and watch it move. That subtlety we shall have to get around in quantum mechanics. But we are first going to learn what the problems are before introducing the complications, and then we shall be in a better position to make corrections, in the light of the more recent knowledge of the subject. We shall, therefore, take a simple point of view about time and space. We know what these concepts are in a rough way, and those who have driven a car know what speed means.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


