Galileo Galilei

The Tale of the Tower

Legend has it that a young, ambitious, and at that moment frustrated mathematics professor climbed to the top of the bell tower in Pisa one day, perhaps in 1591, with a bag of ebony and lead balls. He had advertised to the university community at Pisa that he intended to disprove by experiment a doctrine originated by Aristotle almost two thousand years earlier: that objects fall at a rate proportional to their weight; a ten-pound ball would fall ten times faster than a one pound ball. With a flourish the young professor signaled to the crowd of amused students and disapproving philosophy professors below, selected balls of the same material but with much different weights, and dropped them. Without air resistance (that is, in a vacuum), two balls of different weights (and made of any material) would have reached the ground at the same time. That did not happen in Pisa on that day in 1591, but Aristotle’s ancient principle was clearly violated anyway, and that, the young professor told his audience, was the lesson. The students cheered, and the philosophy professors were skeptical.

        The hero of this tale was Galileo Galilei. He did not actually conduct that “experiment” from the Tower of Pisa, but had he done so it would have been entirely in character. Throughout his life, Galileo had little regard for authority, and one of his perennial targets was Aristotle, the ultimate authority for university philosophy faculties at the time. Galileo's personal style was confrontational, witty, ironic, and often sarcastic. His intellectual style, as the Tower story instructs, was to build his theories with an ultimate appeal to observations.

          The philosophers of Pisa were not impressed with either Galileo or his methods, and would not have been any more sympathetic even if they had witnessed the Tower experiment. To no one’s surprise, Galileo’s contract at the University

Padua

But Galileo knew how to get what he wanted. He had obtained the Pisa post with the help of the Marquis Guidobaldo del Monte, an influential nobleman and competent mathematician. Galileo now aimed for the recently vacated chair of mathematics at the University of Padua, and his chief backer in Padua was Gianvincenzio Pinelli, a powerful influence in the cultural and intellectual life of Padua. Galileo followed Pinelli's advice, charmed the examiners, and won the approval of the Venetian senate (Padua was located in the Republic of Venice, about twenty miles west of the city of Venice). His inaugural lecture was a sensation.

            Padua offered a far more congenial atmosphere for Galileo’s talents and lifestyle than the intellectual backwater he had found in Pisa. In the nearby city of Venice, he found recreation and more aristocratic friends. Galileo's favorite debating partner among these was Gianfrancesco Sagredo, a wealthy nobleman with an eccentric manner Galileo could appreciate. With his wit and flair for polemics, Galileo was soon at home in the city's salons. He took a mistress, Marina Gamba, described by one of Galileo's biographers, James Reston, Jr., as “hot-tempered, strapping, lusty and probably illiterate.” Galileo and Marina had three children: two daughters, Virginia and Livia, and a son, Vincenzo. In later life, when tragedy loomed, Galileo found great comfort in the company of his elder daughter, Virginia.

       During his eighteen years in Padua (1592–1610), Galileo made some of his most important discoveries in mechanics and astronomy. From careful observations, he formulated the “times-squared” law, which states that the vertical distance covered by an object in free fall or along an inclined plane is proportional to the square of the time of the fall. (In modern notation, the equation for free fall is expressed , with s and t the vertical distance and time of the fall, s=gt²/2 and g the acceleration of gravity.) He defined the laws of projected motion with a controlled version of the Tower experiment in which a ball rolled down an inclined plane on a table, then left the table horizontally or obliquely and dropped to the floor. Galileo found that he could make calculations that agreed approximately with his experiments by resolving projected motion into two components, one horizontal and the other vertical. The horizontal component was determined by the speed of the ball when it left the table, and was “conserved” that is, it did not subsequently change. The vertical component, due to the ball's weight, followed the times-squared rule.

       For many years, Galileo had been fascinated by the simplicity and regularity of pendulum motion. He was most impressed by the constancy of the pendulum's “period,” that is, the time the pendulum takes to complete its back-and-forth cycle. If the pendulum’s swing is less than about 30^O, its period is, to a good approximation, dependent only on its length. (Another Galileo legend pictures him as a nineteen-year-old boy in church, paying little attention to the service, and timing with his pulse the swings of an oil lamp suspended on a wire from a high ceiling.) In Padua, Galileo confirmed the constant-period rule with experiments, and then uncovered some of the pendulum’s more subtle secrets.

      In 1609, word came to Venice that spectacle makers in Holland had invented an optical device soon to be called a telescope that brought distant objects much closer. Galileo immediately saw a shining opportunity. If he could build a prototype and demonstrate it to the Venetian authorities before Dutch entrepreneurs arrived on the scene, unprecedented rewards would follow. He knew enough about optics to guess that the Dutch design was a combination of a convex and a concave lens, and he and his instrument maker had the exceptional skill needed to grind the lenses. In twenty-four hours, according to Galileo’s own account, he had a telescope of better quality than any produced by the Dutch artisans. Galileo could have demanded, and no doubt received, a large sum for his invention. But fame and influence meant more to him than money. In an elaborate ceremony, he gave an eight-power telescope to Niccolo Contarini, the doge of Venice. Reston, in Galileo, paints this picture of the presentation of the telescope: ''a celebration of Venetian genius, complete with brocaded advance men, distinguished heralds and secret operatives. Suddenly, the tube represented the flowering of Paduan learning.'' Galileo was granted a large bonus, his salary was doubled, and he was reappointed to his faculty position for life.

       Then Galileo turned his telescope to the sky, and made some momentous, and as it turned out fateful, discoveries. During the next several years, he observed the mountainous surface of the Moon, four of the moons of Jupiter, the phases of Venus, the rings of Saturn (not quite resolved by his telescope), and sunspots. In 1610, he published his observations in The Starry Messenger, which was an immediate sensation, not only in Italy but throughout Europe.

     But Galileo wanted more. He now contrived to return to Tuscany and Florence, where he had spent most of his early life. The grand duke of Tuscany was the young Cosimo de Medici, recently one of Galileo's pupils. To further his cause, Galileo dedicated The Starry Messenger to the grand duke and named the four moons of Jupiter the Medicean satellites. The flattery had its intended effect. Galileo soon accepted an astonishing offer from Florence: a salary equivalent to that of the highest-paid court official, no lecturing duties in fact, no duties of any kind and the title of chief mathematician and philosopher for the grand duke of Tuscany. In Venice and Padua, Galileo left behind envy and bitterness.

Florence and Rome

Again the gregarious and witty Galileo found intellectual companions among the nobility. Most valued now was his friendship with the young, talented, and skeptical Filippo Salviati. Galileo and his students were regular visitors at Salviati's beautiful villa fifteen miles from Florence. But even in this idyll Galileo was restless. He had one more world to conquer: Rome that is, the Church. In 1611, Galileo proposed to the grand duke’s secretary of state an official visit to Rome in which he would demonstrate his telescopes and impress the Vatican with the importance of his astronomical discoveries.

        This campaign had its perils. Among Galileo's discoveries was disturbing evidence against the Church's doctrine that Earth was the center of the universe. The Greek astronomer and mathematician Ptolemy had advocated this cosmology in the second century, and it had long been Church dogma. Galileo could see in his observations evidence that the motion of Jupiter's moons centered on Jupiter, and, more troubling, in the phases of Venus that the motion of that planet centered on the Sun. In the sixteenth century, the Polish astronomer Nicolaus Copernicus had proposed a cosmology that placed the Sun at the center of the universe. By 1611, when he journeyed to Rome, Galileo had become largely converted to Copernicanism. Holy Scripture also regarded the Moon and the Sun as quintessentially perfect bodies; Galileo’s telescope had revealed mountains and valleys on the Moon and spots on the Sun.

        But in 1611 the conflict between telescope and Church was temporarily submerged, and Galileo's stay was largely a success. He met with the autocratic Pope Paul V and received his blessing and support. At that time and later, the intellectual power behind the papal throne was Cardinal Robert Bellarmine. It was his task to evaluate Galileo's claims and promulgate an official position. He, in turn, requested an opinion from the astronomers and mathematicians at the Jesuit Collegio Romano, who reported doubts that the telescope really revealed mountains on the Moon, but more importantly, trusted the telescope's evidence for the phases of Venus and the motion of Jupiter's moons.

        Galileo found a new aristocratic benefactor in Rome. He was Prince Frederico Cesi, the founder and leader of the “Academy of Lynxes,” a secret society whose members were “philosophers who are eager for real knowledge, and who will give themselves to the study of nature, and especially to mathematics.” The members were young, radical, and, true to the lynx metaphor, sharp-eyed and ruthless in their treatment of enemies. Galileo was guest of honor at an extravagant banquet put on by Cesi, and shortly thereafter was elected as one of the Lynxes. Galileo gained many influential friends in Rome and Florence and, inevitably, a few dedicated enemies. Chief among those in Florence was Ludovico della Colombe, who became the self-appointed leader of Galileo's critics. Colombe means “dove” in Italian. Galileo expressed his contempt by calling Colombe and company the “Pigeon League.”

        Late in 1611, Colombe, whose credentials were unimpressive, went on the attack and challenged Galileo to an intellectual duel: a public debate on the theory of floating bodies, especially ice. A formal challenge was delivered to Galileo by a Pisan professor, and Galileo cheerfully responded, “Ever ready to learn from anyone, I should take it as a favor to converse with this friend of yours and reason about the subject.” The site of the debate was the Pitti Palace. In the audience were two cardinals, Grand Duke Cosimo, and Grand Duchess Christine, Cosimo's mother. One of the cardinals was Maffeo Barberini, who would later become Pope Urban VIII and play a major role in the final act of the Galileo drama.

      In the debate, Galileo took the view that ice and other solid bodies float because they are lighter than the liquid in which they are immersed. Colombe held to the Aristotelian position that a thin, flat piece of ice floats in liquid water because of its peculiar shape. As usual, Galileo built his argument with demonstrations. He won the audience, including Cardinal Barberini, when he showed that pieces of ebony, even in very thin shapes, always sank in water, while a block of ice remained on the surface.

The Gathering Storm

The day after his victory in the debate, Galileo became seriously ill, and he retreated to Salviati's villa to recuperate. When he had the strength, Galileo summarized in a treatise his views on floating bodies, and, with Salviati, returned to the study of sunspots. They mapped the motion of large spots as the spots traveled across the sun's surface near the equator from west to east.

      Then, in the spring of 1612, word came that Galileo and Salviati had a competitor. He called himself Apelles. (He was later identified as Father Christopher Scheiner, a Jesuit professor of mathematics in Bavaria.) To Galileo's dismay, Apelles claimed that his observations of sunspots were the first, and explained the spots as images of stars passing in front of the sun. Not only was the interloper encroaching on Galileo's priority claim, but he was also broadcasting a false interpretation of the spots. Galileo always had an inclination to paranoia, and it now had the upper hand. He sent a series of bold letters to Apelles through an intermediary, and agreed with Cesi that the letters should be published in Rome by the Academy of Lynxes. In these letters Galileo asserted for the first time his adherence to the Copernican cosmology. As evidence he recalled his observations of the planets: “I tell you that [Saturn] also, no less than the horned Venus agrees admirably with the great Copernican system. Favorable winds are now blowing on that system. Little reason remains to fear crosswinds and shadows on so bright a guide.”

      Galileo soon had another occasion to proclaim his belief in Copernicanism. One of his disciples, Benedetto Castelli, occupied Galileo’s former post, the chair of mathematics at Pisa. In a letter to Galileo, Castelli wrote that recently he had had a disturbing interview with the pious Grand Duchess Christine. “Her Ladyship began to argue against me by means of the Holy Scripture,” Castelli wrote. Her particular concern was a passage from the Book of Joshua that tells of God commanding the Sun to stand still so Joshua’s retreating enemies could not escape into the night. Did this not support the doctrine that the Sun moved around Earth and deny the Copernican claim that Earth moved and the Sun was stationary?

       Galileo sensed danger. The grand duchess was powerful, and he feared that he was losing her support. For the first time he openly brought his Copernican views to bear on theological issues. First he wrote a letter to Castelli. It was sometimes a mistake, he wrote, to take the words of the Bible literally. The Bible had to be interpreted in such a way that there was no contradiction with direct observations: “The task of wise interpreters is to find true meanings of scriptural passages that will agree with the evidence of sensory experience.” He argued that God could have helped Joshua just as easily under the Copernican cosmology as under the Ptolemaic.

       The letter to Castelli, which was circulated and eventually published, brought no critical response for more than a year. In the meantime, Galileo took more drastic measures. He expanded the letter, emphasizing the primacy of observations over doctrine when the two were in conflict, and addressed it directly to Grand Duchess Christine. “The primary purpose of the Holy Writ is to worship God and save souls,” he wrote. But “in disputes about natural phenomena, one must not begin with the authority of scriptural passages, but with sensory experience and necessary demonstrations.” He recalled that Cardinal Cesare Baronius had once said, “The Bible tells us how to go to Heaven, not how the heavens go.”

       The first attack on Galileo from the pulpit came from a young Dominican priest named Tommaso Caccini, who delivered a furious sermon centering on the miracle of Joshua, and the futility of understanding such grand events without faith in established doctrine. This was a turning point in the Galileo story. As Reston puts it: “Italy’s most famous scientist, philosopher to the Grand Duke of Tuscany, intimate of powerful cardinals in Rome, stood accused publicly of heresy from an important pulpit, by a vigilante of the faith.” Caccini and Father Niccolo Lorini, another Dominican priest, now took the Galileo matter to the Roman Inquisition, presenting as evidence for heresy the letter to Castelli.

      Galileo could not ignore these events. He would have to travel to Rome and face the inquisitors, probably influenced by Cardinal Bellarmine, who had, four years earlier, reported favorably on Galileo’s astronomical observations. But once again Galileo was incapacitated for months by illness. Finally, in late 1615 he set out for Rome.

       As preparation for the inquisitors, a Vatican commission had examined the Copernican doctrine and found that its propositions, such as placing the Sun at the center of the universe, were “foolish and absurd and formally heretical.” On February 25, 1616, the Inquisition met and received instructions from Pope Paul to direct Galileo not to teach or defend or discuss Copernican doctrine. Disobedience would bring imprisonment.

       In the morning of the next day, Bellarmine and an inquisitor presented this injunction to Galileo orally. Galileo accepted the decision without protest and waited for the formal edict from the Vatican. That edict, when it came a few weeks later, was strangely at odds with the judgment delivered earlier by Bellarmine. It did not mention Galileo or his publications at all, but instead issued a general restriction on Copernicanism: “It has come to the knowledge of the Sacred Congregation that the false Pythagorean doctrine, namely, concerning the movement of the Earth and immobility of the Sun, taught by Nicolaus Copernicus, and altogether contrary to the Holy Scripture, is already spread about and received by many persons. Therefore, lest any opinion of this kind insinuate itself to the detriment of Catholic truth, the Congregation has decreed that the works of Nicolaus Copernicus be suspended until they are corrected.”

         Galileo, always an optimist, was encouraged by this turn of events. Despite Bellarmine's strict injunction, Galileo had escaped personal censure, and when the “corrections” to Copernicus were spelled out they were minor. Galileo remained in Rome for three months, and found occasions to be as outspoken as ever. Finally, the Tuscan secretary of state advised him not to “tease the sleeping dog further,” adding that there were “rumors we do not like.”

Comets, a Manifesto, and a Dialogue

       In Florence again, Galileo was ill and depressed during much of 1617 and 1618. He did not have the strength to comment when three comets appeared in the night sky during the last four months of 1618. He was stirred to action, however, when Father Horatio Grassi, a mathematics professor at the Collegio Romano and a gifted scholar, published a book in which he argued that the comets provided fresh evidence against the Copernican cosmology. At first Galileo was too weak to respond himself, so he assigned the task to one of his disciples, Mario Guiducci, a lawyer and graduate of the Collegio Romano. A pamphlet, Discourse on Comets, was published under Guiducci's name, although the arguments were clearly those of Galileo.

      This brought a worthy response from Grassi, and in 1621 and 1622 Galileo was sufficiently provoked and healthy to publish his eloquent manifesto, The Assayer. Here Galileo proclaimed, “Philosophy is written in this grand book the universe, which stands continually open to our gaze. But the book cannot be understood unless one first learns to comprehend the language and to read the alphabet in which it is composed. It is written in the language of mathematics, and its characters are triangles, circles and other geometric figures, without which it is humanly impossible to understand a single word of it; without these, one wanders about in a dark labyrinth.” The Assayer received Vatican approval, and Cardinal Barberini, who had supported Galileo in his debate with della Colombe, wrote in a friendly and reassuring letter, “We are ready to serve you always.” As it turned out, Barberini's good wishes could hardly have been more opportune. In 1623, he was elected pope and took the name Urban VIII.

       After recovering from a winter of poor health, Galileo again traveled to Rome in the spring of 1624. He now went bearing microscopes. The original microscope design, like that of the telescope, had come from Holland, but Galileo had greatly improved the instrument for scientific uses. Particularly astonishing to the Roman cognoscenti were magnified images of insects.

         Shortly after his arrival in Rome, Galileo had an audience with the recently elected Urban VIII. Expecting the former Cardinal Barberini again to promise support, Galileo found to his dismay a different persona. The new pope was autocratic, given to nepotism, long-winded, and obsessed with military campaigns. Nevertheless, Galileo left Rome convinced that he still had a clear path. In a letter to Cesi he wrote, “On the question of Copernicus His Holiness said that the Holy Church had not condemned, nor would condemn his opinions as heretical, but only rash. So long as it is not demonstrated as true, it need not be feared.”

     Galileo's strategy now was to present his arguments hypothetically, without claiming absolute truth. His literary device was the dialogue. He created three characters who would debate the merits of the Copernican and Aristotelian systems, but ostensibly the debate would have no resolution. Two of the characters were named in affectionate memory of his Florentine and Venetian friends, Gianfrancesco Sagredo and Filippo Salviati, who had both died. In the dialogue Salviati speaks for Galileo, and Sagredo as an intelligent layman. The third character is an Aristotelian, and in Galileo’s hands earns his name, Simplicio.

        The dialogue, with the full title Dialogue Concerning the Two Chief World Systems, occupied Galileo intermittently for five years, between 1624 and 1629. Finally, in 1629, it was ready for publication and Galileo traveled to Rome to expedite approval by the Church. He met with Urban and came away convinced that there were no serious obstacles.

         Then came some alarming developments. First, Cesi died. Galileo had hoped to have his Dialogue published by Cesi's Academy of Lynxes, and had counted on Cesi as his surrogate in Rome. Now with the death of Cesi, Galileo did not know where to turn. Even more alarming was an urgent letter from Castelli advising him to publish the Dialogue as soon as possible in Florence. Galileo agreed, partly because at the time Rome and Florence were isolated by an epidemic of bubonic plague. In the midst of the plague, Galileo found a printer in Florence, and the printing was accomplished. But approval by the Church was not granted for two years, and when the Dialogue was finally published it contained a preface and conclusion written by the Roman Inquisitor. At first, the book found a sympathetic audience. Readers were impressed by Galileo's accomplished use of the dialogue form, and they found the dramatis personae, even the satirical Simplicio, entertaining.

         In August 1632, Galileo's publisher received an order from the Inquisition to cease printing and selling the book. Behind this sudden move was the wrath of Urban, who was not amused by the clever arguments of Salviati and Sagredo, and the feeble responses of Simplicio. He even detected in the words of Simplicio some of his own views. Urban appointed a committee headed by his nephew, Cardinal Francesco Barberini, to review the book. In September, the committee reported to Urban and the matter was handed over to the Inquisition.

Trial

After many delays Galileo was once again seriously ill, and the plague had returned Galileo arrived in Rome in February 1633 to defend himself before the Inquisition. The trial began on April 12. The inquisitors focused their attention on the injunction Bellarmine had issued to Galileo in 1616. Francesco Niccolini, the Tuscan ambassador to Rome, explained it this way to his office in Florence: “The main difficulty consists in this: these gentlemen [the inquisitors] maintain that in 1616 he [Galileo] was commanded neither to discuss the question of the earth's motion nor to converse about it. He says, to the contrary, that these were not the terms of the injunction, which were that that doctrine was not to be held or defended. He considers that he has the means of justifying himself since it does not appear at all from his book that he holds or defends the doctrine . . . or that he regards it as a settled question.” Galileo offered in evidence a letter from Bellarmine, which bolstered his claim that the inquisitors’ strict interpretation of the injunction was not valid.

        Historians have argued about the weight of evidence on both sides, and on a strictly legal basis, concluded that Galileo had the stronger case. (Among other things, the 1616 injunction had never been signed or witnessed.) But for th inquisitors, acquittal was not an option. They offered what appeared to be a reasonable settlement: Galileo would admit wrongdoing, submit a defense, and receive a light sentence. Galileo agreed and complied. But when the sentence came on June 22 it was far harsher than anything he had expected: his book was to be placed on the Index of Prohibited Books, and he was condemned to life imprisonment.

Last Act

Galileo's friends always vastly outnumbered his enemies. Now that he had been defeated by his enemies, his friends came forward to repair the damage. Ambassador Niccolini managed to have the sentence commuted to custody under the Archbishop Ascanio Piccolomini of Siena. Galileo's “prison” was the archbishop's palace in Siena, frequented by poets, scientists, and musicians, all of whom arrived to honor Galileo. Gradually his mind returned to the problems of science, to topics that were safe from theological entanglements. He planned a dialogue on “two new sciences,” which would summarize his work on natural motion (one science) and also address problems related to the strengths of materials (the other science). His three interlocutors would again be named Salviati, Sagredo, and Simplicio, but now they would represent three ages of the author: Salviati, the wise Galileo in old age; Sagredo, the Galileo of the middle years in Padua; and Simplicio, a youthful Galileo.

        But Galileo could not remain in Siena. Letters from his daughter Virginia, now Sister Maria Celeste in the convent of St. Matthew in the town of Arcetri, near Florence, stirred deep memories. Earlier he had taken a villa in Arcetri to be near Virginia and his other daughter, Livia, also a sister at the convent. He now appealed to the pope for permission to return to Arcetri. Eventually the request was granted, but only after word had come that Maria Celeste was seriously ill, and more important, after the pope’s agents had reported that the heretic’s comfortable “punishment” in Siena did not fit the crime. The pope’s edict directed that Galileo return to his villa and remain guarded there under house arrest.

       Galileo took up residence in Arcetri in late 1633, and for several months attended Virginia in her illness. She did not recover, and in the spring of 1634, she died. For Galileo this was almost the final blow. But once again work was his restorative. For three years he concentrated on his Discourses on Two New Sciences. That work, his final masterpiece, was completed in 1637, and in 1638 it was published (in Holland, after the manuscript was smuggled out of Italy). By this time Galileo had gone blind. Only grudgingly did Urban permit Galileo to travel the short distance to Florence for medical treatment.

       But after all he had endured, Galileo never lost his faith. “Galileo's own conscience was clear, both as Catholic and as scientist,” Stillman Drake, a contemporary science historian, writes. “On one occasion he wrote, almost in despair, that he felt like burning all his work in science; but he never so much as thought of turning his back on his faith. The Church turned its back on Galileo, and has suffered not a little for having done so; Galileo blamed only some wrong-headed individuals in the Church for that.”

Methods

Galileo's mathematical equipment was primitive. Most of the mathematical methods we take for granted today either had not been discovered or had not come into reliable use in Galileo's time. He did not employ algebraic symbols or equations, or, except for tangents, the concepts of trigonometry. His numbers were always expressed as positive integers, never as decimals. Calculus, discovered later by Newton and Gottfried Leibniz, was not available. To make calculations he relied on ratios and proportionalities, as defined in Euclid's Elements. His reasoning was mostly geometric, also learned from Euclid.

        Galileo's mathematical style is evident in his many theorems on uniform and accelerated motion; here a few are presented and then “modernized” through translation into the language of algebra. The first theorem concerns uniform motion:

If a moving particle, carried uniformly at constant speed, traverses two distances, the time intervals required are to each other in the ratio of these distances.

For us (but not for Galileo) this theorem is based on the algebraic equation s= vt, in which s represents distance, v speed, and t time. This is a familiar calculation. For example, if you travel for three hours (t = 3 hours) at sixty miles per hour (v = 60 miles per hour), the distance you have covered is 180 miles (s = 3 × 60 = 180 miles). In Galileo’s theorem, we calculate two distances, call them s₁ and s₂, for two times, t₁ and t₂, at the same speed, v. The two calculations are

  s₁ = vt₁   and   s₂ = vt₂

Dividing the two sides of these equations into each other, we get the ratio of Galileo's theorem,

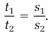
Here is a more complicated theorem, which does not require that the two speeds be equal:

If two particles are moved at a uniform rate, but with unequal speeds, through unequal distances, then the ratio of time intervals occupied will be the product of the ratio of the distances by the inverse ratio of the speeds.

In this theorem, there are two different speeds, v₁ and v₂, involved, and the two equations are

s₁ = v₁t₁   and   s₂ = v₂t₂.

Dividing both sides of the equations into each other again, we have

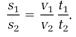
To finish the proof of the theorem, we multiply both sides of this equation by v₂/v₁ and obtain

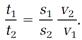
On the right side now is a product of the direct ratio of the distances s₁/s₂ and the inverse ratio of the speeds v₂/v₁, as required by the theorem.

        These theorems assume that any speed v is constant; that is, the motion is not accelerated. One of Galileo’s most important contributions was his treatment of uniformly accelerated motion, both in free fall and down inclined planes.                  “Uniformly” here means that the speed changes by equal amounts in equal time intervals. If the uniform acceleration is represented by a, the change in the speed v in time t is calculated with the equation v = at. For example, if you accelerate your car at the uniform rate a = 5 miles per hour per second for t = 10 seconds, your final speed will be v = 5 × 10 = 50 miles per hour. A second equation, s= at²/2, calculates s, the distance covered in time t under the uniform acceleration a. This equation is not so familiar as the others mentioned. It is most easily justified with the methods of calculus.

        The motion of a ball of any weight dropping in free fall is accelerated in the vertical direction, that is, perpendicular to Earth's surface, at a rate that is conventionally represented by the symbol g, and is nearly the same anywhere on Earth. For the case of free fall, with a = g, the last two equations mentioned are v = gt, for the speed attained in free fall in the time t, and s= gt²/2 for the corresponding distance covered.

       Galileo did not use the equation s= gt²/2 , but he did discover through experimental observations the times-squared (t²) part of it. His conclusion is expressed in the theorem,

    The spaces described by a body falling from rest with a uniformly accelerated motion are to each other as the squares of the time intervals employed in traversing these distances. Our modernized proof of the theorem begins by writing the free-fall equation twice,

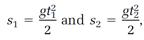
and combining these two equations to obtain

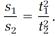
         In addition to his separate studies of uniform and accelerated motion, Galileo also treated a composite of the two in projectile motion. He proved that the trajectory followed by a projectile is parabolic. Using a complicated geometric method, he developed a formula for calculating the dimensions of the parabola followed by a projectile (for example, a cannonball) launched upward at any angle of elevation. The formula is cumbersome compared to the trigonometric method we use today for such calculations, but no less accurate. Galileo demonstrated the use of his method by calculating with remarkable precision a detailed table of parabola dimensions for angles of elevation from 1^o to 89^o.

      In contrast to his mathematical methods, derived mainly from Euclid, Galileo's experimental methods seem to us more modern. He devised a system of units that parallels our own and that served him well in his experiments on pendulum motion. His measure of distance, which he called a punto, was equivalent to 0.094 centimeter. This was the distance between the finest divisions on a brass rule. For measurements of time he collected and weighed water flowing from a container at a constant rate of about three fluid ounces per second. He recorded weights of water in grains (1 ounce = 480 grains), and defined his time unit, called a tempo, to be the time for 16 grains of water to flow, which was equivalent to 1/92 second. These units were small enough so Galileo's measurements of distance and time always resulted in large numbers. That was a necessity because decimal numbers were not part of his mathematical equipment; the only way he could add significant digits in his calculations was to make the numbers larger.

Legacy

Galileo took the metaphysics out of physics, and so begins the story that will unfold in the remaining chapters of this book. As Stephen Hawking writes, “Galileo, perhaps more than any single person, was responsible for the birth of modern science. . . . Galileo was one of the first to argue that man could hope to understand how the world works, and, moreover, that he could do this by observing the real world.” No practicing physicist, or any other scientist for that matter, can do his or her work without following this Galilean advice.

       I have already mentioned many of Galileo’s specific achievements. His work in mechanics is worth sketching again, however, because it paved the way for his greatest successor. (Galileo died in January 1642. On Christmas Day of that same year, Isaac Newton was born.) Galileo's mechanics is largely concerned with bodies moving at constant velocity or under constant acceleration, usually that of gravity. In our view, the theorems that define his mechanics are based on the equations v = gt and s= gt²/2, but Galileo did not write these, or any other, algebraic equations; for his numerical calculations he invoked ratios and proportionality. He saw that projectile motion was a resultant of a vertical component governed by the acceleration of gravity and a constant horizontal component given to the projectile when it was launched. This was an early recognition that physical quantities with direction, now called “vectors,” could be resolved into rectangular components.

          I have mentioned, but not emphasized, another building block of Galileo's mechanics, what is now called the “inertia principle.” In one version, Galileo put it this way: “Imagine any particle projected along a horizontal plane without friction; then we know . . . that this particle will move along this plane with a motion which is uniform and perpetual, provided the plane has no limits.” This statement reflects Galileo's genius for abstracting a fundamental idealization from real behavior. If you give a real ball a push on a real horizontal plane, it will not continue its motion perpetually, because neither the ball nor the plane is perfectly smooth, and sooner or later the ball will stop because of frictional effects. Galileo neglected all the complexities of friction and obtained a useful postulate for his mechanics. He then applied the postulate in his treatment of projectile motion. When a projectile is launched, its horizontal component of motion is constant in the absence of air resistance, and remains that way, while the vertical component is influenced by gravity.

         Galileo's mechanics did not include definitions of the concepts of force or energy, both of which became important in the mechanics of his successors. He had no way to measure these quantities, so he included them only in a qualitative way. Galileo's science of motion contains most of the ingredients of what we now call “kinematics.” It shows us how motion occurs without defining the forces that control the motion. With the forces included, as in Newton's mechanics, kinematics becomes “dynamics.”

          All of these specific Galilean contributions to the science of mechanics were essential to Newton and his successors. But transcending all his other contributions was Galileo's unrelenting insistence that the success or failure of a scientific theory depends on observations and measurements. Stillman Drake leaves us with this trenchant synopsis of Galileo's scientific contributions: “When Galileo was born, two thousand years of physics had not resulted in even rough measurements of actual motions. It is a striking fact that the history of each science shows continuity back to its first use of measurement, before which it exhibits no ancestry but metaphysics. That explains why Galileo's science was stoutly opposed by nearly every philosopher of his time, he having made it as nearly free from metaphysics as he could. That was achieved by measurements, made as precisely as possible with means available to Galileo or that he managed to devise.”