مع أنَّ الفوتونات ليس لها كتلة، اتضح أنها ما زالت متأثرة بالجاذبية. ومن الأفضل ألا نعتبر ذلك ناجما عن قوة ما، بل بالأحرى عن انحناء نسيج الزمكان. صحيح أننا عادة ما نظن أنَّ الفوتون يتحرك في خط مستقيم، وهذا ما نستمد منه فكرة «شعاع الضوء». ولكن عند تحركه عبر نسيج مُنحنٍ من الزمكان سيتبع مسارًا يُعرف بأنه خط جيوديسي. ومع أنَّ دلالة كلمة «جيوديسي» تُوحي بأنها مرتبطة بكوكب الأرض فقط، فإنَّ الخط الجيوديسي (الذي اشتق اسمه من علم الجيوديسيا، أي قياس خواص الأرض على سطح كوكبنا) مفهوم مهم في وصف طبيعة نسيج الزمكان عبر الكون كله. إذا لم يكن الفضاء منحنيًا (أي كان مُتَّسقًا تمامًا مع الشكل الهندسي اليومي الذي ربما تعلمناه في المدرسة من إقليدس أو أحد العلماء الذين جاءوا من بعده)، فحينئذٍ سيكون الخط الجيوديسي هو «المسار المستقيم الذي سيقطعه شعاع ضوئي. لكن أقصر مسافة بين نقطتين، التي تمثل المسار الذي يريد» شعاع ضوئي أن يسلكه، معروفة بمصطلح «الخط الجيوديسي الصفري». أما في الفضاء المنحني، فأقصر مسافة بين نقطتين ليست ما نعتبرها مستقيمة،

لكنَّ «الخطوط الجيوديسية خطوط مستقيمة في فضاءاتٍ مُنحنية.» يمكن كذلك وصف الخط المستقيم بأنه المسار الذي تسلكه بمواصلة التحرُّك في الاتجاه نفسه. وإذا أردتَ مثالًا على أنَّ الهندسة على الأسطح المنحنية مختلفة بشدة، فانظر إلى خطوط الطول على كرة. فأي خطَّين متجاورين من خطوط الطول (متوازيين عند خط الاستواء) سيلتقيان في نقطة عند القطب، كما هو موضّح في شكل 2-5 ولكن في الفضاء المسطح، لن تلتقي الخطوط المتوازية إلا عند اللانهاية (وفقًا لمسلَّمة إقليدس الأخيرة).

شكل 2-5: تكون خطوط الطول على كرة ما متوازية عند خط الاستواء، وتلتقي في نقطة عند القطبين.

وفي الواقع، حيثما يكون نسيج الزمكان مُنحنيًا، وليكن بسبب وجود كتلة مثلا، يتجلى ذلك الانحناء في المسار الذي سيسلكه شعاع ضوئي أو «جُسَيم اختبار» (أداة ذهنية استخدمها الفيزيائيون) يستطيع التحرك بحرية دون تأثير من أي قوة خارجية، بين حدثين. وينبغي اعتبار الحدثين نقطتين في نسيج الزمكان الرباعي الأبعاد، على أن يُرمز إلى كلتيهما بالصيغة (t، x، y، z).

تُخبرنا قاعدة تُسمى الدالة المترية بالكيفية التي تقيس بها الساعات والمساطر الفواصل بين الأحداث في نسيج الزمكان ، وتُتيح الأساس الذي يمكن الاستناد عليه في حل المسائل في الهندسة. ومن أبسط أمثلة الدالة المترية نظرية فيثاغورس، التي توضح كيفية حساب المسافة بين نقطتين تقعان في المستوى. وتُوضّح لنا حلول معادلات المجال التي وضعها أينشتاين كيف نحسب قيم الدالة المترية لنسيج الزمكان عندما يكون توزيع المادة معروفًا. ونستخدم هذا لإنشاء خطوط معبرة عن خطوط الكون الحقيقي الجيوديسية. فعلى سبيل المثال، كان أحد أول الأدلة الرصدية على النسبية العامة هو انحناء الضوء النجمي بفعل الشمس، الذي قيس في أثناء كسوف شمسي (فهو وقت مناسب لفحص المواضع الظاهرة للنجوم القريبة من قرص الشمس لأنَّ الضوء المنبعث من القرص يكون محجوبا بالقمر حينئذ، وهي فرصة اغتنمها السير آرثر إدينجتون في عام 1919). وكتلة الشمس تُسبِّب انحناء نسيج الزمكان. وبذلك فإن أقصر مسار (أي الخط الجيوديسي) من نجم بعيد إلى تلسكوب على الأرض ليس خطًا مستقيما، بل منحن بفعل مجال جاذبية الشمس، كما هو موضح في شكل 2-6.

شكل 2-6: كتلة الشمس تسبب تشوها او انحناء في نسيج الزمكان.

وصحيح أنَّ انحناء الضوء النجمي يُظهر أنَّ الفضاء منحن، لكن النظرية العامة لأينشتاين تُخبرنا بأنَّ نسيج الزمكان هو الذي يتّسم بالانحناء في الواقع. لذا قد نتوقع أن هذه الكتلة لها بعض التأثيرات الغريبة على الزمان أيضًا. وفي الحقيقة، فحتي مجال جاذبية كوكب الأرض كافٍ ليجعل الساعات الموجودة على سطح كوكب الأرض تدق بوتيرة أبطأ قليلا من التي تدق بها في الفضاء السحيق، ومع أنَّ ذلك التأثير ضئيل (إذ يبلغ نحو جزء واحد في المليار)، فهو قابل للقياس. غير أنَّ تأثيرات الجاذبية بالقرب من أفق الحدث المحيط بالثقب الأسود أقوى بكثير. وبذلك فإنَّ الزمن يمضي بشكل مختلف بالقرب من الثقب الأسود، حتى الثقب غير الدوار الذي يُعد أبسط حالات الثقوب السوداء، مقارنةً بالكيفية التي يمضي بها على بعد مسافة كبيرة من الثقب الأسود. هذا تأثير حقيقي ولا يعتمد على كيفية قياس الوقت (سواء بساعة ذرية، أو بساعة رقمية مثلا). إذ ينجم مباشرة عن انحناء نسيج الزمكان الناتج من الكتلة، والذي يُوجه المخاريط الضوئية نحو الكتلة. يُبين شكل 2-7 التأثير العام.

تؤثر الثقوب السوداء تأثيرًا عميقًا في اتجاهات المخاريط الضوئية. فعندما يقترب جُسَيم من الثقب الأسود، يميل مخروطه الضوئي المستقبلي أكثر فأكثر نحو الثقب الأسود، بحيث يتحول الثقب الأسود تدريجيًّا إلى جزءٍ من مُستقبله المحتوم. وعندما يمر الجسيم عبر أُفق الحدث، تنتهي مساراته المستقبلية المحتملة كلها داخل الثقب الأسود. وفي نطاق أفق الحدث فقط، يكون ميل المخروط الضوئي كبيرا لدرجة أنَّ أحد جوانبه يُصبح موازيًا لأفق الحدث، ويقع المستقبل كله ضمن نطاق أفق الحدث؛ فالهروب من الثقب الأسود غير ممكن. ويوضح شكل 2-7 أيضًا هذه النقطة بالمثال: فهو أساسًا تمثيل لبعض مخططات الزمكان المحلية، لأن تجميع المخاريط الضوئية يُتيح لك فهم الظروف المحلية التي يمر بها جسيم اختبار موجود في مواقع مختلفة في هذا الشكل، يتقدم الزمن مع الاتجاه إلى أعلى الصفحة، ولذا فهذا المخطط البياني يُعطي كذلك فكرةً عن كيفية تكون الثقب الأسود ونموه بفعل المادة المنهارة الساقطة نحوه.

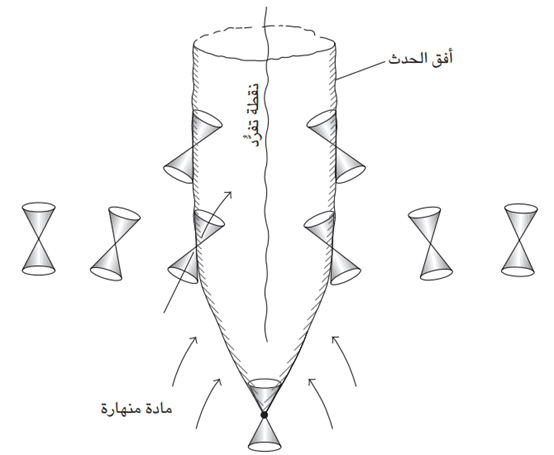
شكل 2-7: مخطط نسيج الزمكان المحيط بثقب أسود يبين كيف أنَّ المخاريط الضوئية المستقبلية الخاصة بأجسام على أفق الحدث تقع داخل نطاق أفق الحدث.

وكنجوم ميشيل ولابلاس المظلمة والتي استطاعت الحفاظ على أنظمة من الكواكب في مدارات حولها على غرار مجموعتنا الشمسية، نعرف فقط أنَّ الثقب الأسود قريب بسبب ما لديه من قوة شد قائمة على الجاذبية. وربما قد يجعلك هذا تظن أنَّ الخاصية الوحيدة التي تُميز الثقب الأسود هي: كتلته. ولكن في الواقع، تتأثر خصائص الثقب الأسود تأثرًا شديدًا بما إذا كان يدور أم لا.