طريقة القيمة الكبرى M لحل مسائل البرمجة الخطية (Big M)
المؤلف:
ا.د. ابو القاسم مسعود الشيخ
المصدر:
بحوث العمليات
الجزء والصفحة:
102-113
30-1-2022
8206
طريقة القيمة الكبرى M لحل مسائل البرمجة الخطية (Big M)
لقد شرحنا سابقاً أسباب إضافة المتغير الصناعي (Artificial variable) وذلك لإنشاء الحل الابتدائي لمسائل البرمجة الخطية بالإضافة إلى أن وجود هذا المتغير بقيمة موجبة تعني أن الحل الحالي ليس حلاً ملموساً لأي مسألة ويمكن التخلص من المتغير الصناعي وذلك بإضافة إلى دالة الهدف بموافق ذو قيمة كبيرة جداً وغير مشجعة، كمتغير في القيود وتصبح بذلك إمكانية التخلص منه سريعة جداً.
ولتوضيح هذه الظاهرة مع شرط أن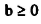 
بإضافة المتغير الصناعي في حالة التساوي
إن بداية المتغيرات الأساسية للحل يمكن أن تعطي على هيئة:
xa = b
ودالة الهدف طورت بطريقة الطرد المتغير الصناعي وذلك بإضافة قيمة كبيرة خيالية لمعاقبة وجود المتغير الصناعي في الحل وبالتحديد يسمى (M) وعليه يعاد صياغة المسألة على النحو التالي:
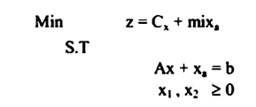
حيث M قيمة موجبة كبيرة جداً، والصفر Mixa يمكن تعليله كعقوبة يدفعها الحل الذي يحتوي على 
بالرغم من أن xa = b , x = 0 ، كبداية للحل فقط وبإضافة M الكبيرة تسعى طريقة السمبلكس وحدها لإزالة xa (المتغير أو المتغيرات الصناعية).
ولتوضيح هذه الطريقة نقدم المثال التالي:
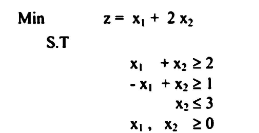
أولاً: يجب إضافة x3, x4, x5 slacks ومتغيرات صناعية x7 ، x6 وتصبح المسألة على الصيغة التالية:
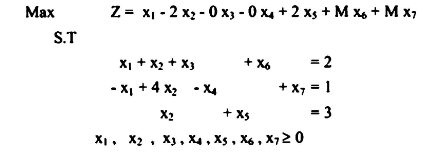
,يمكن كتابتها في جداول السمبلكس على النحو التالي:
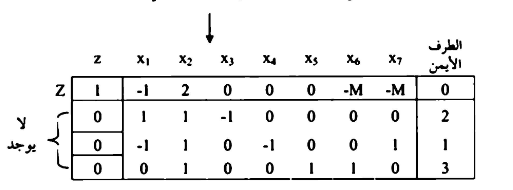
بضرب الصف رقم (1) والصف رقم (2) وجمعها على الصف صغر
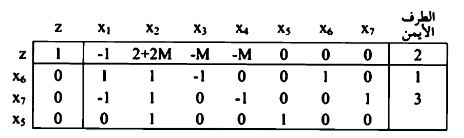
بالنظر في صف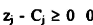 
بالنسبة x2 وعليه نختار x2 للدخول في الحل الأساسي وتخرج x7 وفق القاعدة :
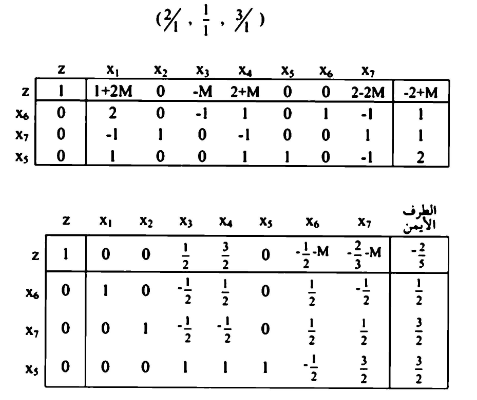
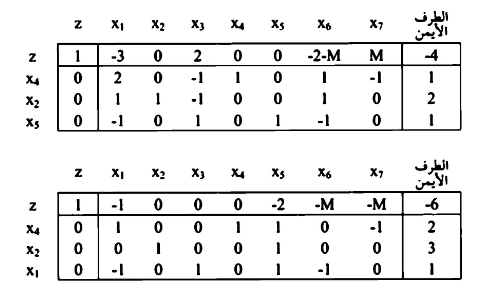
بما ان كل 
كل متغير لا يوجد في الحل الأساسي.
آخر جدول تعتبر الحل الأمثل (optimum).
ويوضح الرسم الحل البياني للمسألة.
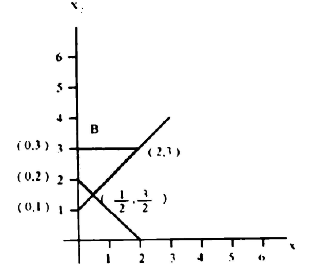
مثال 6.3 :
(في حالة عدم وجود حل متاح للمسألة (Infeasible solution)
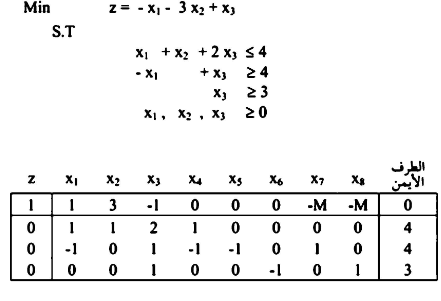
بضرب الصف 2 و 3 في m وإضافتهما إلى الصف0
بالنظر في الصف 0 نلاحظ وجود قيم لغير المتغيرات الأساسية.
مثال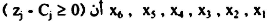 
وبالتالي باختيار أكبر قيمة موجبة لتقرير المتغير الذي يدخل الحل وباستخدام القاعدة بقسمة 
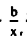حيث R العمود المختار.
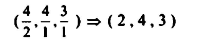
وباعتبار 2 قيمة موجودة عليه تدخل x3 وتخرج x4.
بما ان m قيمة موجة وكبيرة جداً وان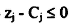 
لجميع المتغيرات غير الأساسية في الحل، عليه فإن شروط الحصول على الحل الأمثل قد تحققت ، ولكن بما ان المتغيرات الصناعية x8 , x7 موجودة بالحل وعند قيم موجبة عالية وفقاً للقاعدة فإن الحل خيالي وغير موجود.
مثال 6.4 الحل موجود ولكن غير محدود المساحة:
(Unbounded optimal solution)
بإضافة متغيرات صناعية للتساوي حسب القاعدة هما x5 ، x6 وبالتالي يعاد كتابة المسألة على النحو الآتي:
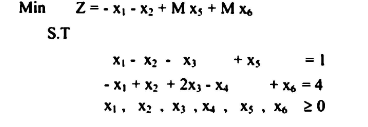
ويمكن نقل المسألة على هيئة الجداول على النحو الآتي:
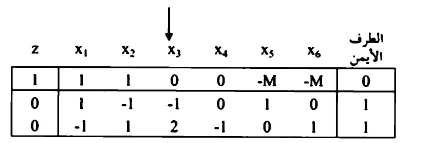
يضرب الصف الأول والثاني في صفر وإضافتها إلى الصف صفر
ونلاحظ أن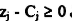 
C المقابلة لـ x2 قيمة موجبة لكم 
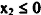عليه فإن المسألة ذات حل محدود ولأن المتغيرات الصناعية x5 ، x6 آلت إلى الصفر.
مثال 6.5
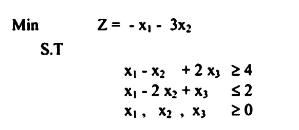
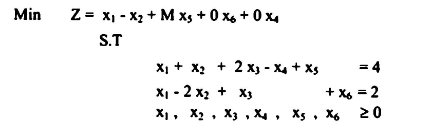
عليه يمكن كتابة المسألة على هيئة الجداول على النحو الاتي:
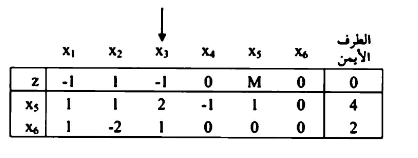
يضرب الصف الأول والثاني في صفر وإضافتها إلى الصف (0).
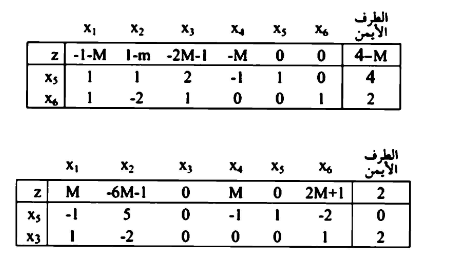
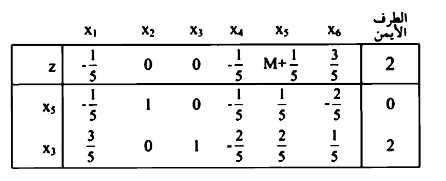
بما أن 
الا والمتغيرات الصناعية كلها آلات إلى الصفر، فإن الحل ذ مساحة غير محدودة. وتوجد قيمة موجبة 
مقابلة x4
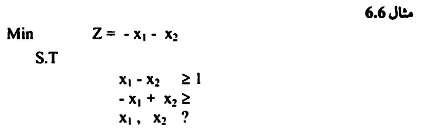
بإضافة x3 , x4 Slack وإضافة المتغيرات الصناعية x6 , x5 للوصول إلى حالة التساوي وبالتالي يمكن كتابة المسألة على النحو التالي:
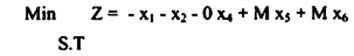
يضرب الصف الأول والصف الثاني في M وإضافتها إلى الصف صفر.
نلاحظ أن الصف صفر الذي يحتوي على zj - Cj توجد قيم المتغيرات الغير داخلة في أكبر من الصفر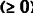 
ولا يمكن إدخال أي متغير آخر لتحسين الحل نظراً لعدم إمكانية تحسين الحل وفق القاعدة 
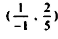لا يجوز اختيار أحد العناصر ويدل على عدم توفر حل يحقق هذه المسألة.
الاكثر قراءة في بحوث العمليات
اخر الاخبار
اخبار العتبة العباسية المقدسة
