تاريخ الرياضيات
الاعداد و نظريتها
تاريخ التحليل
تار يخ الجبر
الهندسة و التبلوجي
الرياضيات في الحضارات المختلفة
العربية
اليونانية
البابلية
الصينية
المايا
المصرية
الهندية
الرياضيات المتقطعة
المنطق
اسس الرياضيات
فلسفة الرياضيات
مواضيع عامة في المنطق
الجبر
الجبر الخطي
الجبر المجرد
الجبر البولياني
مواضيع عامة في الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
الهندسة المستوية
الهندسة غير المستوية
مواضيع عامة في الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
معادلات تفاضلية
معادلات تكاملية
مواضيع عامة في المعادلات
التحليل
التحليل العددي
التحليل العقدي
التحليل الدالي
مواضيع عامة في التحليل
التحليل الحقيقي
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
500AD
500-1499
1000to1499
1500to1599
1600to1649
1650to1699
1700to1749
1750to1779
1780to1799
1800to1819
1820to1829
1830to1839
1840to1849
1850to1859
1860to1864
1865to1869
1870to1874
1875to1879
1880to1884
1885to1889
1890to1894
1895to1899
1900to1904
1905to1909
1910to1914
1915to1919
1920to1924
1925to1929
1930to1939
1940to the present
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان
طرق حل مسائل البرمجة الخطية بواسطة طريقة السمبلكس Simplex Method :أمثلة تطبيقية:
المؤلف:
ا.د. ابو القاسم مسعود الشيخ
المصدر:
بحوث العمليات
الجزء والصفحة:
77-83
29-1-2022
18266
+
-
20
طرق حل مسائل البرمجة الخطية بواسطة طريقة السمبلكس Simplex Method :أمثلة تطبيقية:
مثال 1: إذا اعتبرنا المعادلتين التاليتين. فأوجد الحل الابتدائي للمتغيرات
إذا أضفنا المتغير الفارق (Slack variable)، فيمكن كتابة المعادلات على النحو الآتي:
ويمكن معاملة المعادلات التي تحتوي على أكبر من (2) بواسطة إضافة المتغير الصناعي الفائض (artificial variable) حيث أن المتغير الصناعي لا توجد له أي قيمة طبيعية أو معنوية والغرض من إضافته الحصول الفوري على حل ابتدائي وبعدها تبدأ طريقة السمبلكس التي سوف توضح فيها بعد:
يمكن كتابتها على الصورة: (5.13)
أما في حالة
للحصول على حل ابتدائي وذلك بإضافة المتغير الصناعي فقط:
والامثلة الاتية يمكن ان تعطي توضيح اكثر.
مثال 2:
حول المعادلات الاتية إلى صورة جاهزة لاستخدامها للحل بطريقة السمبلكس.
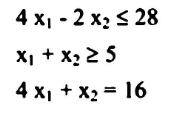
الحل:
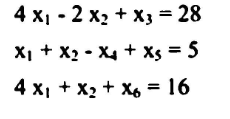
طبقاً للخطوات السابقة ووفقاً للمعادلة فإن الحل الابتدائي:
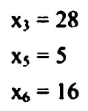
2- أثر تحميل المعادلات على دالة الهدف:
إن اختيار المتغيرات التي يتخذ عليها القرار يؤثر مباشرة على قيمة دالة الهدف وهذا ينطبق سواء على إضافة (slack variable) او المتغير الصناعي
(artificial variable)
عليه فإن أي دالة يضاف إليها هذين النوعين من المتغيرات سوف تعاد كتابتها على النحو الاتي:
نلاحظ ان الجزء ci xi هو دالة الهدف الاصلية.
أما الجزء c5 x5 هو اثر إضافة على دالة الهدف.
أما الجزء الثالث CA XA فهو أثر إضافة المتغير الصناعي على دالة الهدف.
مثال3:
إذا أعطيت مسألة البرمجة الخطية التالية. المطلوب تغييرها على صيغة قابلة للحل بطريقة السمبلكس.
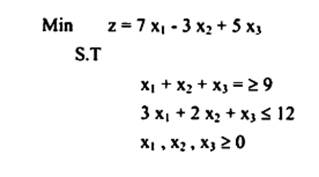
الحل:
ويمكن صياغة هذه المسألة بصورة أسهل استعمالاً
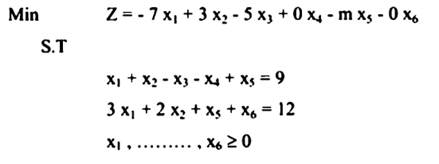
حيث:
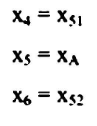
3- بعض التعريفات والرموز المهمة لطريقة السمبلكس :
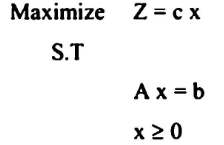
حيث c مصفوفة الصف الواحد (n x 1)
A مصفوفة m x n
B مصفوفة عمود واحد (1 x m )
مثال 4 :
إذا اعتبرنا مسألة البرمجة الخطية التالية حيث:
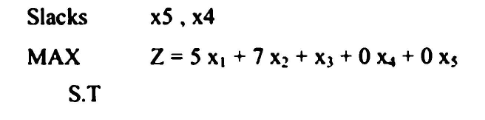
هذه المسألة يمكن كتابتها على النحو التالي:
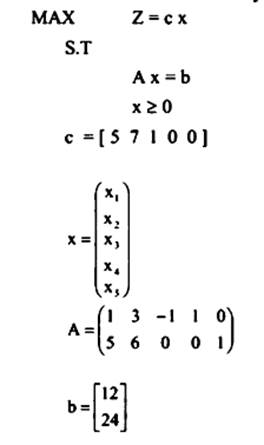
أي مصفوفة B تسمى حل ابتدائي إذا حققت حل المعادلة A x = b مع الأخذ في الاعتبار ان قيم لـ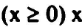 
وإذا خالف هذا الشرط يسمى حل غير منظور.
أي ان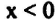 
الحل الابتدائي لأي مسألة برمجة خطية
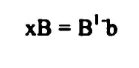
حيث XB
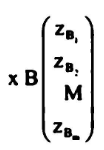
مثال 5 :
في المثال السابق إذا اخترنا
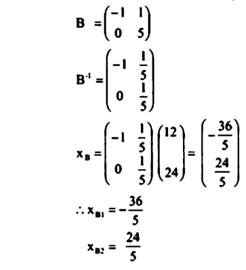
وبما ان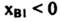 
هذا الحل غير منظور
الاكثر قراءة في بحوث العمليات
اخر الاخبار
اخبار العتبة العباسية المقدسة
الآخبار الصحية
مواضيع ذات صلة
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
