صياغة مسائل البرمجة الخطيةProblem Formulation: امثلة

مثال 1:

مجمع الدواجن بالمنطقة الوسطى يقوم بتغذية 20000 فراخ لمدة 8 أسابيع قبل نقلها إلى السوق. علما بأن تغذية هذه الفراخ يختلف وفقاً للعمر والاستهلاك الأسبوعي لذي يبلغ تقريباً 455 غرام. ولكي يتحقق الوزن المستهدف في الأسبوع الثامن. يجب أن تكون تركيبة الغذاء محتوية على نسبة معينة من البروتين.

المطلوب:

إيجاد الكمية المثالية من خلطة المواد الغذائية المستخدمة لتحقيق الوزن المطلوب وبأقل تكلفة ممكنة، والجدول رقم (2-3) يوضح تركيبة المواد وتكاليفها.

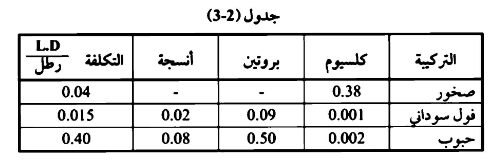
علماً بأن خلطة التركيبة الغذائية يشترك فيها الآتي:

1- نسبة الكالسيوم 0.8% على الأقل ولا تزيد عن 1.2 %.

2- البروتين 22% على الأقل.

3- البروتين 5% على الأكثر.

الحل:

 = X1 كمية الصخور في الخلطة رطل.

X2  = كمية الفول السوداني في الخلطة رطل.

  X3 = كمية الحبوب في الخلطة رطل.

باعتبار ان عدد الفراخ 20,000 ، وكل فراخ يحتاج إلى رطل.

رطل 20,000 = 1 × 20,000

رطل 20,000 = x1 + x2 + x3

الشرط الأول :

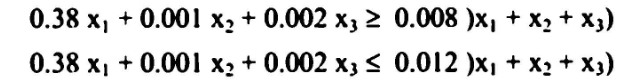
والتي يمكن كتابتها بصورة أبسط على النحو الآتي:

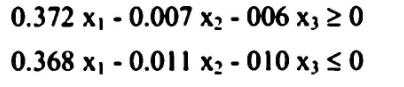
والدالة الهدف :

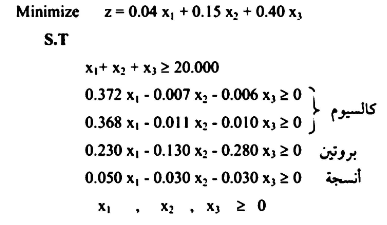
مثال2 : قررت إحدى شركات الاستثمارات الداخلية استثمار مبلغ 50,000 د.ل في ثلاثة مشاريع هي بناء عقارات وإدارة مشروع زراعي وتجارة سلع.

وقد قدر عائد أرباحها السنوي بنسبة 7% ، 9% ، 14% ، على التوالي ومن ضمن مخططات الشركة الاستثمارية.

1- الحصول على العائد السنوي بما لا يقل عن 5000 د.ل .

2- توفير 10,000 على الأقل.

3- التقوير من تجارة السلع الداخلية لا يزيد عن التوفير في باقي الاستثمارات .

4- التوفير في بناء العقارات لا يقل عن 5000 د.ل ولا يزيد عن 5,000 د.ل.

المطلوب :

كيفية توزيع المبلغ المستثمر 50,000 في المشاريع الثلاثة بحيث يحقق أكبر استثمار يمكن.

الحل:

نفرض أن:

X1 = الاستثمار في العقارات د.ل.

x2 = الاستثمار في إدارة المشروع الزراعي د.ل.

x3 = الاستثمار في تجارة السلع د.ل

أولاً: لتحقيق العائد السنوي من المشاريع الاستثمارية الثلاثة:

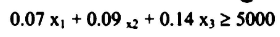
ثانياً: لتحقيق الاستثمار في العقارات

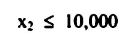
ثالثاً: التوفير في تجارة السلع الداخلية لا يزيد عن التوفير في بناء العقارات

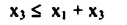
رابعاً: قيود التوفير في العقارات

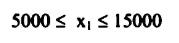
خامساً: مجموع الاستشارات لا يزيد عن 50,000 د.ل

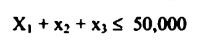
سادساً: شروط الاستثمارات لا تكون سالبة

مثال 3:

قامت شركة النقل الريفي داخل أحدى مدن الجماهيرية الليبية بدراسة لغرض توفير المواصلات داخل المدينة مع مراعاة تقليل وتصغير عدد الحافلات التي تقوم بنقل المواطنين على أن تكون وسيلة النقل متوفرة خلال الأربع وعشرين ساعة. ومن - خلال الدراسة الإحصائية التي قامت بها مجموعة من المهندسين أفادت الدراسة بعدد الحافلات اللازمة خلال فترات مختلفة خلال اليوم وقسمت هذه الفترات إلى ست فترات کما موضح بالشكل (1-3).

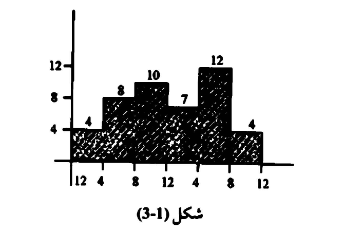
المطلوب:

احسب عدد الحافلات اللازمة للتشغيل خلال الفترات الست المختلفة والتي تستوعب الطلبية المناسبة وبأقل عدد ممكن من الحافلات.

إذا افترضنا أن:

X1 ، X2 ، X3 ، X4 ، X5 ، X6 هو عدد الحافلات اللازمة للتشغيل في بداية كل فترة، أي أن:

X1= عدد الحافلات التي تبدأ العمل الساعة 12:01

X2 = عدد الحافلات التي تبدأ العمل الساعة 4:01 صباحاً

x3 = عدد الحافلات التي تبدأ العمل الساعة 8:01

X4 = عدد الحافلات التي تبدأ العمل الساعة 12:01

X5= عدد الحافلات التي تبدأ العمل الساعة 4:01

X6 = عدد الحافلات التي تبدأ العمل الساعة 8:01

ويوضح الشكل رقم (2-3) التداخل الذي يحصل بين الفترات.

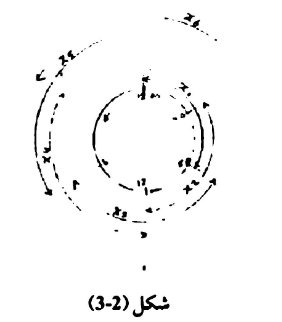
عدد الحافلات التي تشتغل خلال كل الفترات وبأقل عدد ممكن هو الهدف

تقوم الشركة العربية الليبية للاسمنت بإنتاج كميات كبيرة من الاسمنت من مصانع مختلفة موزعة في كل من سوق الخميس، الخمس، درنة، بنغازي.

ويوزع إنتاج هذه المصانع على مراكز مختلفة للتسويق داخل الجماهيرية الليبية مثال بنغازي – سرت - مصراته - طرابلس - سبها.

فإذا فرضنا مصان الاسمنت M ومراكز التوزيع N

حيث:                     i=1,2,3,..... m

                                  j=1,2,3..... n             

وأن تكلفة وحدة النقل من المصنع إلى المركز التوزيع هي cij

وأن سعر الإنتاج في المصنع : هي ai.

وأن سعر الطلبية في المركز زهي bj.

43

المطلوب:

كيفية نقل كميات الأسمنت من المصنع : إلى مركز j   بأقل تكلفة ممكنة وتعرف هذه المشكلة باسم مشكلة النقل.

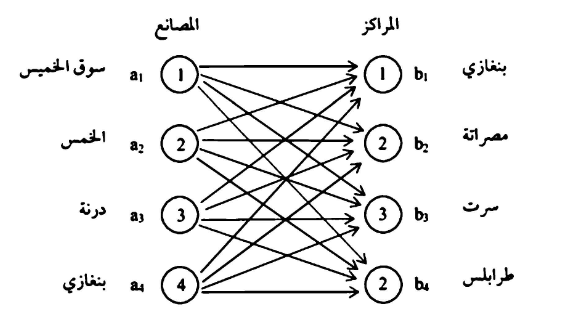
ويمكن صياغة المسألة على نموذج برمجة خطية وذلك على النحو الآتي:

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد

مواضيع ذات صلة

النموذج الثنائي لمسائل البرمجة الخطيةDuality in Linear Programming:تحليل الحساسية (Sensitivity Analysis):

النموذج الثنائي لمسائل البرمجة الخطيةDuality in Linear Programming:طريقة حل المسائل الثنائية بواسطة السمبلكس

النموذج الثنائي لمسائل البرمجة الخطيةDuality in Linear Programming: طرق حساب النموذج الأولي والثنائي:

النموذج الثنائي لمسائل البرمجة الخطيةDuality in Linear Programming:أهمية العلاقة ما بين النموذج الاولي والنموذج الثنائي وحساباتها:

النموذج الثنائي لمسائل البرمجة الخطيةDuality in Linear Programming:العلاقة بين النموذج الأول والنموذج الثنائي:

النموذج الثنائي لمسائل البرمجة الخطيةDuality in Linear Programming:المقدمة:

بعض الظواهر الشاذة لحل مسائل البرمجة الخطية بواسطة طريقة السمبلكس :الانحراف

بعض الظواهر الشاذة لحل مسائل البرمجة الخطية بواسطة طريقة السمبلكس: تكرار العهد

بعض الظواهر الشاذة لحل مسائل البرمجة الخطية بواسطة طريقة السمبلكس :المتغيرات الغير محددة

طريقة القيمة الكبرى M لحل مسائل البرمجة الخطية (Big M)

الخطوات الأساسية لطريقة السمبلكس -2

حل مسألة البرمجة الخطية بطريقة جداول السمبلكس