استخدام الطريقة البيانية في حل نموذج البرمجة الخطية Graphical Solution of Linear Programming :امثلة:

امثلة على كيفية تمثيل بواسطة الرسم البياني:

إذا اعتبرنا القيود الآتية:

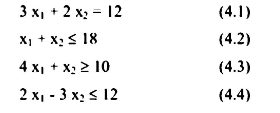
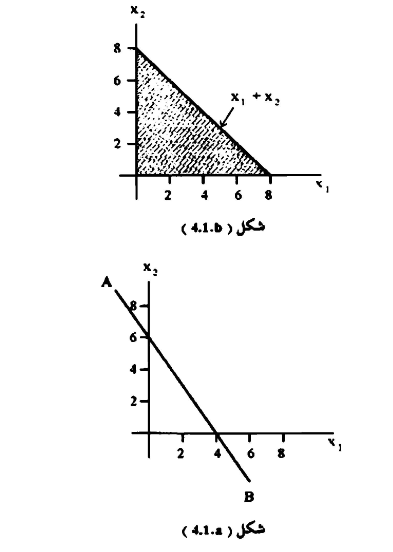
ومن خلال الرقم (4.1) نلاحظ أن القيد (4.1) يرسم على هيئة خط مستقیم کما هو موضح في الشكل (a.4.1) وأن أي نقطة على الخط AB يجب أن تحقق معادلة القيد، وبما أنه من المعروف في شروط مسائل البرمجة الخطة أن كل المتغيرات لها قيمة أكبر من أو تساوي (ك) صفر. عليه يجب اعتبار المساحة التي من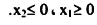

نلاحظ أن القيد (4.2) أقل من كما هو موضح بالشكل (4.1.b) والقيد (4.3) أكبر من كما هو موضح بالشكل (4.1.c) أقل من كما هو موضح بالشكل (4.1.d) وأن المساحة المظللة تعني أن أي نقطة على حدودها أو داخلها يجب أن تحقق المعادلة.

إن هذا المثال رسمت فيه كل معادلة على حدة، ولكن عندما يتم رسم ا المعادلات في شكل واحد سوف تحدد فيها المساحة المشتركة بين المعادلات التي تحقق كل المعادلات في آن واحد ونعرف المساحة المشتركة بـ (Feasible area) وهي المساحة التي يتاح فيها حل المسألة سواء كانت تعظيم أو تصغير.

ويمكن تلخيص الخطوات اللازمة للرسم على النحو الآتي:

1- نعرف محاور المتغيرات وفقاً لمسميات المتغيرات (مثل x2,x1).

2- ارسم معادلات القيود، حقق خط في حالة (=) أو مساحة في حالة  أو 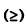 المرافقة لكل قيد.

3- عرف أو حدد المنطقة الممكنة (Feasible area) بين القيود والتي تسمى مساحة الحل والتي أي نقطة فيها تحقق المعادلات وأن أي نقطة خارج هذه المساحة لا تحقق المعادلات تسمى خارج الحل أو (infeasible) بمعنى غير منظورة من وجهة نظر الحل.

4 عرف النقاط الركنية والتي مرشحة أن تكون نقطة الحل الأمثل ( (optimu.

5- أحسب قيمة الحل الأمثل (optimum solution) وذلك بحساب قيمة دالة الهدف لكل نقطة مرشحة للحل في الخطوة الرابعة. وعليه فإن لنقطة التي تحقق أكبر قيمة ممكنة في حالة التعظيم أو أقل قيمة ممكنة لدالة الهدف في حالة التصغير تعتبر نقطة الحل وأن القيمة المصاحبة لها الدالة الهدف هي الحل الأمثل، وسوف نوضح هذه الخطوات في الأمثل القادمة.

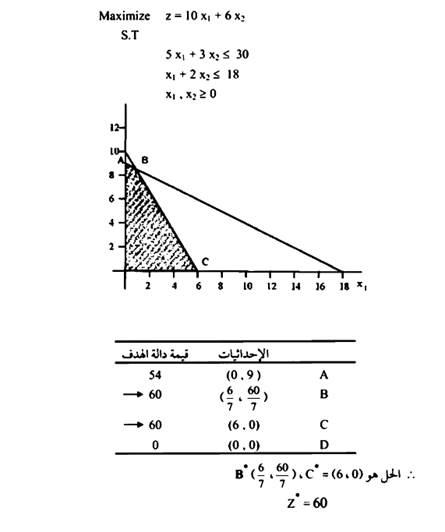
مثال 2:

مسألة تعظيم (Maximization Problem)

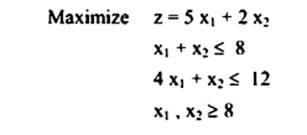
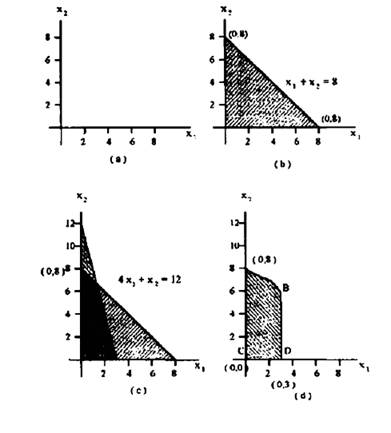
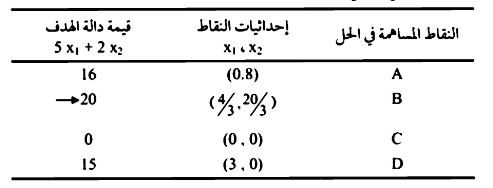
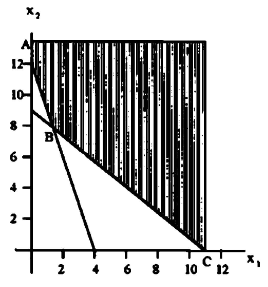
الواضح من الرسم (d) أن النقاط المشاركة في الحل هي النقاط  d, c, b, aلاختيار الحل الأمثل:

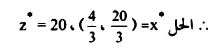
مسألة تصغير (Minimization problem)

يتشابه استخدام الطريقة البيانية في حالة مشكلة التصغير مثل تقليل التكاليف (Cost minimization) مع استخدامها في حالة مشكلة التعظيم والفارق الوحيد سوف يكون في خطوة اختيار الحل الأمثل.

 أوجد قيمة ,x2 ، x1 إذا كان

يمكن رسم القيود على النحو التالي:

وبمعايرة دالة الهدف عند النقاط C, B, A في المساحة غير المغلقة (Unbounded) أو غير محصورة.

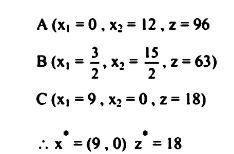
يعني النقطة التي يوجد عندها الحل الأمثل.

مثال4:

مسألة تعظيم ومساحة الحل غير محصورة.

من الواضح أن الحل الأمثل هو أعظم قيمة ممكنة وبالتالي فإن نقطة الحل هي :

مثال5 :

في حالة وجود أكثر من حل مثالي للمسألة (Alternative optimum solution). أوجد قيمة x₂ , x₁ إذا كان

مثال 6:

القيد المتكرر (Redundant Constraints).

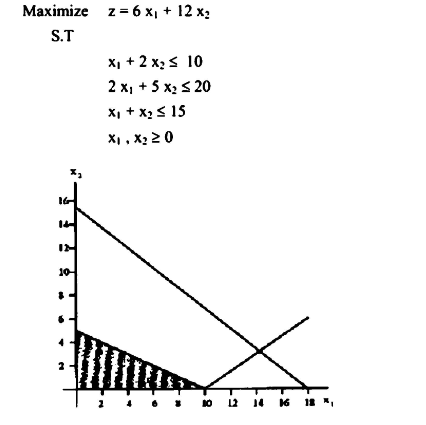
نلاحظ أن القيد الوحيد الذي يمكن أن يعتمد عليه في الحل هو القيد

(x₁  = 2x≤ 10)

وكذلك قيود عدم السلبية

أما القيد الثاني والثالث فلا تأثير لها على مساحة الحل.

مثال 7:

المسألة التي يوجد لها أكثر من حل (Alternative optimum solution). أوجد قيمة X₁ ، X₂ إذا كان

يتضح من الشكل السابق أنه لا توجد مساحة مشتركة بين القيود، وبالتالي لا يوجد حل للمسألة.

مثال 8: (المسألة التي لا يوجد لها حل)

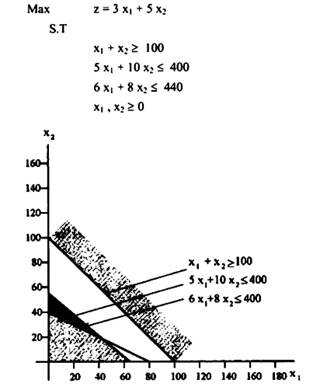
نلاحظ من الرسم أن الثلاثة قيود الموضحة أعلاه لا توجد بينها مساحة مشتركة، بمعنى آخر لا توجد قيمة للمتغير X1 ، X2 تحقق كل المعادلات وعليه تسمى هذه المسألة بالمسألة التي ليس لها حل (Infusible problem)