

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
تعريف مفردات البرمجة الخطية
المؤلف:
ا.د. ابو القاسم مسعود الشيخ
المصدر:
بحوث العمليات
الجزء والصفحة:
26-28
26-1-2022
2751
تعريف مفردات البرمجة الخطية
1- التغيرات (Variables)
يقصد بالمتغير الذي يرمز له بقيمة مثل (n........... xi (j= 1,2,3,
2- المغفور للتحكم فيه (Continuous variable)
هو متغير تحت تصرف من يتخذ القرار.
3- التغير المستمر (Continuous variable)
هو متغير ذو قيمة محصورة بين حدود عظمى ودنيا.
4- العام الشماع (Discrete variable)
هو المتغير الذي يأخذ قيم موصوفة بدرجات معلومات
مثال X لا يمكن أن تأخذ القيم 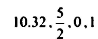
5- المقابر المقطع (Linear Function)
هي الدوال أو المعادلات التي لا تأخذ في أسها إلا واحد فقط.
مثال x + x وليس X1 log x2 . وتعتبر هذه الدوال من ذات المتغير المستمر
6- الدوال في الخطية (Non liner Function):
عكس الدوال الخطية ويمكن أن يكون أسها أقل و أكثر من (1).
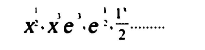
وتعتبر هذه الدوال من الدوال ذات المتغير المتقطع.
7- النمط الرياضي (Mathematical model)
هو نمط يحدد العلاقة بين متغيرات وثابت تحاكي واقع أي نظام، والنمط الرياضي الخطي هو الذي يحوي على معادلات خطية فقط.
8- المعادلات (Equations)
ويمكن تمثيلها بواسطة الآتي:
F(x) = b
ويعني هذا أن بعض الدوال تحتوي على متغيرات في الطرف الشمالي.
X = X1 , X2 X3 ……....... Xn
وعلى طرف يمين يساوي (b)
9- الغير متعادلات (Inequalities)
ويقصد بها المعادلات التي طرفها الشمالي لا يساوي الطرف الأيمن فقط، بل يزيد أو يقل عنه. ويمكن التعبير عنها رياضياً على النحو التالي:
f(x) ≤ b
f(x) > b
10- الأهداف (Objectives)
ويمكن تمثيلها رياضياً بواسطة المعادلة التالية:
Minimize f(x) or maximize f(x)
وهو تعبير عن تصغير التكاليف أو المسافات أو تعظيم الربح أو الإنتاج.
11- القيود (Constraints)
هي عبارة عن معادلات يجب أن تحقق رياضياً في ظل الهدف، ويمكن أن يعبر عنها رياضياً.
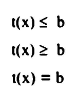
ويعتمد على حالة الإنتاجية.
 الاكثر قراءة في بحوث العمليات
الاكثر قراءة في بحوث العمليات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















