


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-1-2022
Date: 12-1-2022
Date: 11-1-2022
|
Let 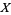 be an infinite set of urelements, and let
be an infinite set of urelements, and let 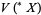 be an enlargement of the superstructure
be an enlargement of the superstructure 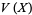 . Let
. Let 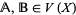 be finitary algebras with finitely many operations, and let
be finitary algebras with finitely many operations, and let 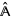 and
and 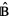 be their extension monads in
be their extension monads in 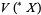 . Let
. Let 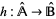 be a homomorphism. Then
be a homomorphism. Then 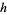 is internally extendable provided that there is an internal subalgebra
is internally extendable provided that there is an internal subalgebra 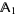 of
of 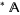 which contains
which contains 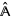 and there is a homomorphism
and there is a homomorphism 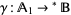 such that if
such that if 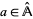 , then
, then 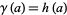 .
.
For a homomorphism 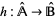 , the following are equivalent:
, the following are equivalent:
1. 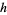 is internally extendable and
is internally extendable and ![h[A]](https://mathworld.wolfram.com/images/equations/InternallyExtendableHomomorphism/Inline18.gif) is a subalgebra of
is a subalgebra of 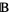 ,
,
2. For some homomorphism 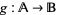 ,
, 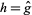 is the restriction to
is the restriction to 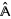 of
of 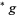 .
.
REFERENCES:
Albeverio, S.; Fenstad, J.; Hoegh-Krohn, R.; and Lindstrøom, T. Nonstandard Methods in Stochastic Analysis and Mathematical Physics. New York: Academic Press, 1986.
Hurd, A. E. and Loeb, P. A. An Introduction to Nonstandard Real Analysis. Orlando, FL: Academic Press, 1985.
Insall, M. "Nonstandard Methods and Finiteness Conditions in Algebra." Zeitschr. f. Math., Logik, und Grundlagen d. Math. 37, 525-532, 1991.
Insall, M. "Some Finiteness Conditions in Lattices Using Nonstandard Proof Methods." J. Austral. Math. Soc. 53, 266-280, 1992.
Luxemburg, W. A. J. Applications of Model Theory to Algebra, Analysis, and Probability. New York: Holt, Rinehart, and Winston, 1969.
Robinson, A. Nonstandard Analysis. Amsterdam, Netherlands: North-Holland, 1966.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|