


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات Any set which can be put in a one-to-one correspondence with the natural numbers (or integers) so that a prescription can be given for identifying its members one at a time is called a countably infinite (or denumerably infinite) set. Once one countable set 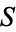 is given, any other set which can be put into a one-to-one correspondence with
is given, any other set which can be put into a one-to-one correspondence with 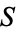 is also countable. Countably infinite sets have cardinal number aleph-0.
is also countable. Countably infinite sets have cardinal number aleph-0.
Examples of countable sets include the integers, algebraic numbers, and rational numbers. Georg Cantor showed that the number of real numbers is rigorously larger than a countably infinite set, and the postulate that this number, the so-called "continuum," is equal to aleph-1 is called the continuum hypothesis. Examples of nondenumerable sets include the real, complex, irrational, and transcendental numbers.
REFERENCES:
Courant, R. and Robbins, H. "The Denumerability of the Rational Number and the Non-Denumerability of the Continuum." §2.4.2 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 79-83, 1996.
Jeffreys, H. and Jeffreys, B. S. Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, p. 10, 1988.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|