Quota System

A generalization of simple majority voting in which a list of quotas 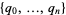 specifies, according to the number of votes, how many votes an alternative needs to win (Taylor 1995). The quota system declares a tie unless for some 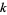, there are exactly  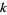tie votes in the profile and one of the alternatives has at least  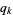votes, in which case the alternative is the choice.

Let 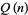 be the number of quota systems for  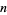voters and  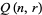the number of quota systems for which 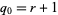, so

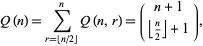(1)

where 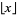 is the floor function. This produces the sequence of central binomial coefficients 1, 2, 3, 6, 10, 20, 35, 70, 126, ... (OEIS A001405). It may be defined recursively by  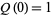and

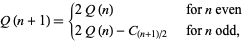(2)

where 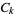 is a Catalan number (Young et al. 1995). The function  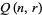satisfies

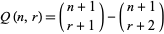(3)

for 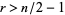 (Young et al. 1995).  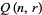satisfies the quota rule.

REFERENCES:

Sloane, N. J. A. Sequence A001405/M0769 in "The On-Line Encyclopedia of Integer Sequences."

Taylor, A. Mathematics and Politics: Strategy, Voting, Power, and Proof. New York:Springer-Verlag, 1995.

Young, S. C.; Taylor, A. D.; and Zwicker, W. S. "Counting Quota Systems: A Combinatorial Question from Social Choice Theory." Math. Mag. 68, 331-342, 1995.