


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-10-2021
Date: 23-8-2021
Date: 10-1-2016
|
Let 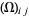 be the resistance distance matrix of a connected graph
be the resistance distance matrix of a connected graph 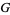 on
on 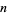 nodes. Then Foster's theorems state that
nodes. Then Foster's theorems state that
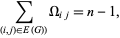 |
where 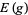 is the edge set of
is the edge set of 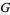 , and
, and
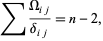 |
where the latter sum runs over all pairs of adjacent edges 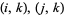 and
and 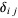 is the vertex degree of the vertex
is the vertex degree of the vertex 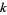 common to those edges (Palacios 2001).
common to those edges (Palacios 2001).
REFERENCES:
Foster, R. M. "The Average Impedance of an Electrical Network." In Contributions to Applied Mechanics (Reissner Anniversary Volume). Ann Arbor, MI: Edwards Brothers, pp. 333-340, 1949.
Foster, R. M. "An Extension of a Network Theorem Contributions to Applied Mechanics." IRE Trans. Cir. Th. 8, 75-76, 1961.
Klein, D. J. and Randić, M. "Resistance Distance." J. Math. Chem 12, 81-95, 1993.
Palacios, J. L. "Closed-Form Formulas for Kirchhoff Index." Int. J. Quant. Chem. 81, 135-140, 2001.
Tetali, P. "Random Walks and the Effective Resistance of Networks." J. Theor. Prob. 4, 101-109, 1991.
Tetali, P. "An Extension of Foster's Network Theorem." Combin. Prob. Comp. 3, 421-427, 1994.
Weinberg, L. "Kirchhoff's 'Third and Fourth Laws." IRE Trans. Cir. Th. 5, 8-30, 1958.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
تضاريس شبيهة بـ"الجبنة السويسرية".. حفرة غامضة على المريخ
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|