


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-8-2021
Date: 3-10-2021
Date: 1-12-2021
|
 |
 |
 |
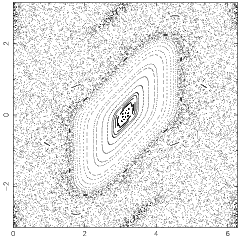 |
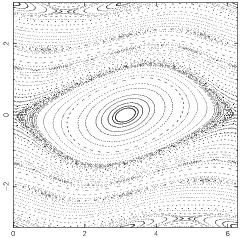
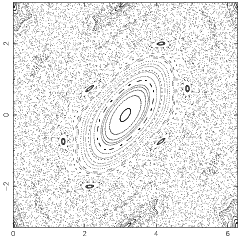
A two-dimensional map also called the Taylor-Greene-Chirikov map in some of the older literature and defined by
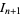 |
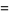 |
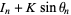 |
(1) |
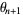 |
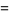 |
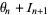 |
(2) |
 |
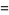 |
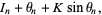 |
(3) |
where 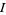 and
and 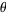 are computed mod
are computed mod 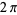 and
and 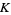 is a positive constant. Surfaces of section for various values of the constant
is a positive constant. Surfaces of section for various values of the constant 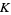 are illustrated above.
are illustrated above.
An analytic estimate of the width of the chaotic zone (Chirikov 1979) finds
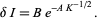 |
(4) |
Numerical experiments give 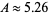 and
and 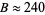 . The value of
. The value of 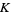 at which global chaos occurs has been bounded by various authors. Greene's Method is the most accurate method so far devised.
at which global chaos occurs has been bounded by various authors. Greene's Method is the most accurate method so far devised.
| author | bound | exact | approx. |
| Hermann | 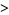 |
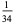 |
0.029411764 |
| Celletti and Chierchia (1995) | 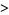 |
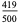 |
0.838 |
| Greene | 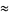 |
- | 0.971635406 |
| MacKay and Percival (1985) |  |
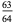 |
0.984375000 |
| Mather | 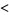 |
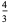 |
1.333333333 |
Fixed points are found by requiring that
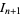 |
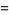 |
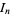 |
(5) |
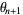 |
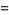 |
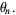 |
(6) |
The first gives 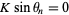 , so
, so 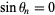 and
and
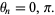 |
(7) |
The second requirement gives
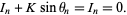 |
(8) |
The fixed points are therefore 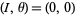 and
and 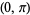 . In order to perform a linear stability analysis, take differentials of the variables
. In order to perform a linear stability analysis, take differentials of the variables
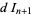 |
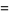 |
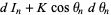 |
(9) |
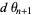 |
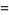 |
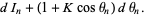 |
(10) |
In matrix form,
![[deltaI_(n+1); deltatheta_(n+1)]=[1 Kcostheta_n; 1 1+Kcostheta_n][deltaI_n; deltatheta_n].](https://mathworld.wolfram.com/images/equations/StandardMap/NumberedEquation4.gif) |
(11) |
The eigenvalues are found by solving the characteristic equation
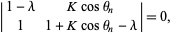 |
(12) |
so
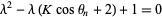 |
(13) |
![lambda_+/-=1/2[Kcostheta_n+2+/-sqrt((Kcostheta_n+2)^2-4)].](https://mathworld.wolfram.com/images/equations/StandardMap/NumberedEquation7.gif) |
(14) |
For the fixed point 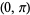 ,
,
 |
 |
![1/2[2-K+/-sqrt((2-K)^2-4)]](https://mathworld.wolfram.com/images/equations/StandardMap/Inline46.gif) |
(15) |
 |
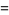 |
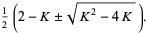 |
(16) |
The fixed point will be stable if 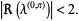 Here, that means
Here, that means
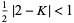 |
(17) |
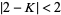 |
(18) |
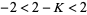 |
(19) |
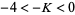 |
(20) |
so 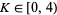 . For the fixed point (0, 0), the eigenvalues are
. For the fixed point (0, 0), the eigenvalues are
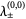 |
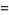 |
![1/2[2+K+/-sqrt((K+2)^2-4)]](https://mathworld.wolfram.com/images/equations/StandardMap/Inline54.gif) |
(21) |
 |
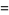 |
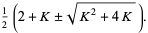 |
(22) |
If the map is unstable for the larger eigenvalue, it is unstable. Therefore, examine 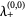 . We have
. We have
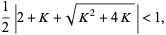 |
(23) |
so
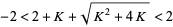 |
(24) |
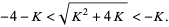 |
(25) |
But 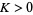 , so the second part of the inequality cannot be true. Therefore, the map is unstable at the fixed point (0, 0).
, so the second part of the inequality cannot be true. Therefore, the map is unstable at the fixed point (0, 0).
REFERENCES:
Celletti, A. and Chierchia, L. "A Constructive Theory of Lagrangian Tori and Computer-Assisted Applications." Dynamics Rep. 4, 60-129, 1995.
Chirikov, B. V. "A Universal Instability of Many-Dimensional Oscillator Systems." Phys. Rep. 52, 264-379, 1979.
MacKay, R. S. and Percival, I. C. "Converse KAM: Theory and Practice." Comm. Math. Phys. 98, 469-512, 1985.
Rasband, S. N. "The Standard Map." §8.5 in Chaotic Dynamics of Nonlinear Systems. New York: Wiley, pp. 11 and 178-179, 1990.
Tabor, M. "The Hénon-Heiles Hamiltonian." §4.2.r in Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, pp. 134-135, 1989.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
شعبة فاطمة بنت أسد (عليها السلام) تنظم دورة تخصصية في أحكام التلاوة
|
|
|