


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-11-2021
Date: 13-10-2021
Date: 19-12-2021
|

Rule 188 is one of the elementary cellular automaton rules introduced by Stephen Wolfram in 1983 (Wolfram 1983, 2002). It specifies the next color in a cell, depending on its color and its immediate neighbors. Its rule outcomes are encoded in the binary representation 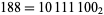 . This rule is illustrated above together with the evolution of a single black cell it produces after 15 steps (Wolfram 2002, p. 55).
. This rule is illustrated above together with the evolution of a single black cell it produces after 15 steps (Wolfram 2002, p. 55).
The mirror image, complement, and mirror complement are rules 230, 194, and 152, respectively.
Starting with a single black cell, successive generations 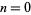 , 1, ... are given by interpreting the numbers 1, 3, 5, 15, 29, 55, 93, 247, 477, ... (OEIS A118173) in binary, namely 1, 011, 00101, 0001111, 000011101, ... (OEIS A118174). The
, 1, ... are given by interpreting the numbers 1, 3, 5, 15, 29, 55, 93, 247, 477, ... (OEIS A118173) in binary, namely 1, 011, 00101, 0001111, 000011101, ... (OEIS A118174). The 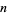 th iteration has generating function
th iteration has generating function
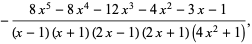 |
(1) |
and closed form
![a(n)={1/(30)[55·2^n+3i(2i)^n-14] for n odd; 1/(15)[25·2^n+3(2i)^n-13] for n even.](https://mathworld.wolfram.com/images/equations/Rule188/NumberedEquation2.gif) |
(2) |
REFERENCES:
Sloane, N. J. A. Sequences A118173 and A118174 in "The On-Line Encyclopedia of Integer Sequences."
Wolfram, S. "Statistical Mechanics of Cellular Automata." Rev. Mod. Phys. 55, 601-644, 1983.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 55, 90, and 952, 2002.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|