Neighborhood

"Neighborhood" is a word with many different levels of meaning in mathematics.

One of the most general concepts of a neighborhood of a point 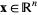 (also called an epsilon-neighborhood or infinitesimal open set) is the set of points inside an 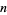-ball with center  and radius 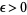. A set containing an open neighborhood is also called a neighborhood.

The graph neighborhood of a vertex 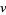 in a graph is the set of all the vertices adjacent to  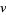generally including  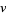itself. More generally, the 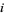th neighborhood of  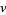is the set of all vertices that lie at the distance  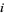from 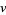. The subgraph induced by the neighborhood of a graph from vertex  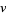(again, most commonly including  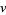itself) is called the neighborhood graph (or sometimes "ego graph" in more recent literature).

REFERENCES:

Balakrishnan, R. and Ranganathan, K. "Vertex Cuts and Edge Cuts." §3.1 in A Textbook of Graph Theory. New York: Springer-Verlag, p. 3, 1999.

Buckley, F. and Harary, F. Distance in Graphs. Redwood City, CA: Addison-Wesley, p. 167, 1990.