


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-8-2021
Date: 2-7-2017
Date: 11-5-2021
|
A topology that is "potentially" a metric topology, in the sense that one can define a suitable metric that induces it. The word "potentially" here means that although the metric exists, it may be unknown.
In fact, there are sufficient criteria on the topology that assure the existence of such a metric even if this is not explicitly given. An example of an existence theorem of this kind is due to Urysohn (Kelley 1955, p. 125), who proved that a regular T1-space whose topology has a countable basis is metrizable.
Conversely, a metrizable space is always 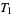 and regular, but the condition on the basis has to be weakened since in general, it is only true that the topology has a basis which is formed by countably many locally finite families of open sets.
and regular, but the condition on the basis has to be weakened since in general, it is only true that the topology has a basis which is formed by countably many locally finite families of open sets.
Special metrizability criteria are known for T2-spaces. A compact 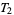 -space is metrizable iff the set of all elements
-space is metrizable iff the set of all elements 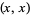 of
of 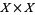 is a zero set (Willard 1970, p. 163). The continuous image of a compact metric space in a Hausdorff space is metrizable. (Willard 1970, p. 166). This implies in particular that a distance can be defined on every path in a T2-space.
is a zero set (Willard 1970, p. 163). The continuous image of a compact metric space in a Hausdorff space is metrizable. (Willard 1970, p. 166). This implies in particular that a distance can be defined on every path in a T2-space.
REFERENCES:
Cullen, H. F. "Metrizable Spaces and Uniformizable Spaces." Ch. 4 in Introduction to General Topology. Boston, MA: Heath, pp. 141-209, 1968.
Kelley, J. L. General Topology. New York: Van Nostrand, 1955.
Willard, S. General Topology. Reading, MA: Addison-Wesley, 1970.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|