Witten's Equations

For a connection 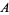 and a positive spinor 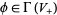, Witten's equations (also called the Seiberg-Witten invariants) are given by

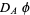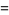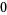			(1)
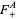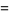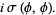			(2)

The solutions are called monopoles and are the minima of the functional

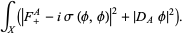(3)

REFERENCES:

Cipra, B. "A Tale of Two Theories." What's Happening in the Mathematical Sciences, 1995-1996, Vol. 3. Providence, RI: Amer. Math. Soc., pp. 14-25, 1996.

Donaldson, S. K. "The Seiberg-Witten Equations and 4-Manifold Topology." Bull. Amer. Math. Soc. 33, 45-70, 1996.

Kotschick, D. "Gauge Theory is Dead!--Long Live Gauge Theory!" Not. Amer. Math. Soc. 42, 335-338, 1995.

Seiberg, N. and Witten, E. "Monopoles, Duality, and Chiral Symmetry Breaking in 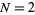 Supersymmetric QCD." Nucl. Phys. B 431, 581-640, 1994.

Witten, E. "Monopoles and 4-Manifolds." Math. Res. Let. 1, 769-796, 1994.