


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 6-5-2021
Date: 16-7-2021
Date: 25-7-2021
|
In algebraic topology, a 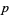 -skeleton is a simplicial subcomplex of
-skeleton is a simplicial subcomplex of 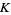 that is the collection of all simplices of
that is the collection of all simplices of 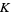 of dimension at most
of dimension at most 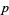 , denoted
, denoted 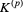 .
.

The graph obtained by replacing the faces of a polyhedron with its edges and vertices is therefore the skeleton of the polyhedron. The polyhedral graphs corresponding to the skeletons of Platonic solids are illustrated above. The number of topologically distinct skeletons 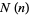 with
with 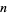 graph vertices for
graph vertices for 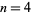 , 5, 6, ... are 1, 2, 7, 18, 52, ... (OEIS A006869).
, 5, 6, ... are 1, 2, 7, 18, 52, ... (OEIS A006869).
REFERENCES:
Gardner, M. Martin Gardner's New Mathematical Diversions from Scientific American. New York: Simon and Schuster, p. 233, 1966.
Hatcher, A. Algebraic Topology. Cambridge, England: Cambridge University Press, 2002.
Munkres, J. R. Elements of Algebraic Topology. New York: Perseus Books Pub., 1993.
Sloane, N. J. A. Sequence A006869/M1748 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
دراسة تستعرض آلام السجناء السياسيين في حقبة البعث المجرم في العراق
|
|
|