


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-4-2021
Date: 24-2-2021
Date: 27-3-2021
|
Let 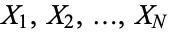 be a set of
be a set of 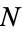 independent random variates and each
independent random variates and each 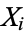 have an arbitrary probability distribution
have an arbitrary probability distribution 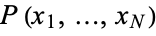 with mean
with mean 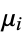 and a finite variance
and a finite variance 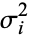 . Then the normal form variate
. Then the normal form variate
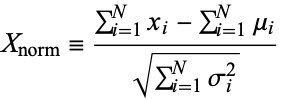 |
(1) |
has a limiting cumulative distribution function which approaches a normal distribution.
Under additional conditions on the distribution of the addend, the probability density itself is also normal (Feller 1971) with mean 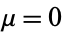 and variance
and variance 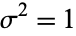 . If conversion to normal form is not performed, then the variate
. If conversion to normal form is not performed, then the variate
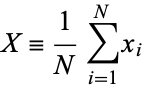 |
(2) |
is normally distributed with 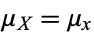 and
and 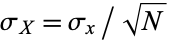 .
.
Kallenberg (1997) gives a six-line proof of the central limit theorem. For an elementary, but slightly more cumbersome proof of the central limit theorem, consider the inverse Fourier transform of 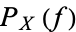 .
.
](https://mathworld.wolfram.com/images/equations/CentralLimitTheorem/Inline12.gif) |
 |
 |
(3) |
 |
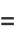 |
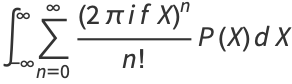 |
(4) |
 |
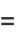 |
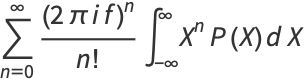 |
(5) |
 |
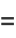 |
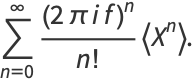 |
(6) |
Now write
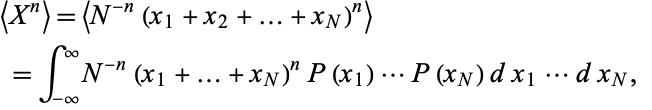 |
(7) |
so we have
](https://mathworld.wolfram.com/images/equations/CentralLimitTheorem/Inline24.gif) |
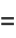 |
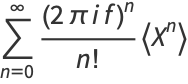 |
(8) |
 |
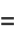 |
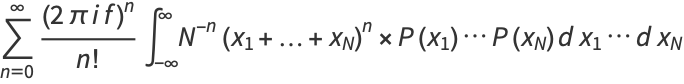 |
(9) |
 |
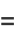 |
![int_(-infty)^inftysum_(n=0)^(infty)[(2piif(x_1+...+x_N))/N]^n1/(n!)P(x_1)...P(x_N)dx_1...dx_N](https://mathworld.wolfram.com/images/equations/CentralLimitTheorem/Inline32.gif) |
(10) |
 |
 |
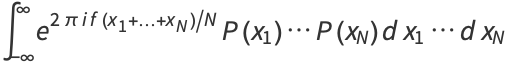 |
(11) |
 |
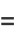 |
![[int_(-infty)^inftye^(2piifx_1/N)P(x_1)dx_1]×...×[int_(-infty)^inftye^(2piifx_N/N)P(x_N)dx_N]](https://mathworld.wolfram.com/images/equations/CentralLimitTheorem/Inline38.gif) |
(12) |
 |
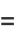 |
![[int_(-infty)^inftye^(2piifx/N)P(x)dx]^N](https://mathworld.wolfram.com/images/equations/CentralLimitTheorem/Inline41.gif) |
(13) |
 |
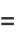 |
![{int_(-infty)^infty[1+((2piif)/N)x+1/2((2piif)/N)^2x^2+...]P(x)dx}^N](https://mathworld.wolfram.com/images/equations/CentralLimitTheorem/Inline44.gif) |
(14) |
 |
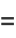 |
![[1+(2piif)/N<x>-((2pif)^2)/(2N^2)<x^2>+O(N^(-3))]^N](https://mathworld.wolfram.com/images/equations/CentralLimitTheorem/Inline47.gif) |
(15) |
 |
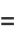 |
![exp{Nln[1+(2piif)/N<x>-((2pif)^2)/(2N^2)<x^2>+O(N^(-3))]}.](https://mathworld.wolfram.com/images/equations/CentralLimitTheorem/Inline50.gif) |
(16) |
Now expand
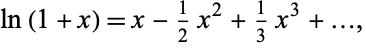 |
(17) |
so
](https://mathworld.wolfram.com/images/equations/CentralLimitTheorem/Inline51.gif) |
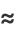 |
![exp{N[(2piif)/N<x>-((2pif)^2)/(2N^2)<x^2>+1/2((2piif)^2)/(N^2)<x>^2+O(N^(-3))]}](https://mathworld.wolfram.com/images/equations/CentralLimitTheorem/Inline53.gif) |
(18) |
 |
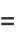 |
![exp[2piif<x>-((2pif)^2(<x^2>-<x>^2))/(2N)+O(N^(-2))]](https://mathworld.wolfram.com/images/equations/CentralLimitTheorem/Inline56.gif) |
(19) |
 |
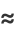 |
![exp[2piifmu_x-((2pif)^2sigma_x^2)/(2N)],](https://mathworld.wolfram.com/images/equations/CentralLimitTheorem/Inline59.gif) |
(20) |
since
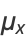 |
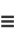 |
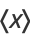 |
(21) |
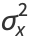 |
 |
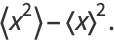 |
(22) |
Taking the Fourier transform,
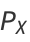 |
 |
![int_(-infty)^inftye^(-2piifx)F^(-1)[P_X(f)]df](https://mathworld.wolfram.com/images/equations/CentralLimitTheorem/Inline68.gif) |
(23) |
 |
 |
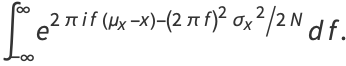 |
(24) |
This is of the form
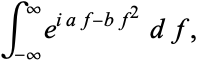 |
(25) |
where 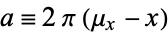 and
and 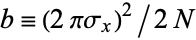 . But this is a Fourier transform of a Gaussian function, so
. But this is a Fourier transform of a Gaussian function, so
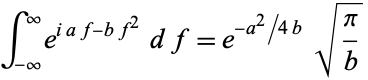 |
(26) |
(e.g., Abramowitz and Stegun 1972, p. 302, equation 7.4.6). Therefore,
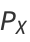 |
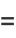 |
![sqrt(pi/(((2pisigma_x)^2)/(2N)))exp{(-[2pi(mu_x-x)]^2)/(4((2pisigma_x)^2)/(2N))}](https://mathworld.wolfram.com/images/equations/CentralLimitTheorem/Inline76.gif) |
(27) |
 |
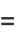 |
![sqrt((2piN)/(4pi^2sigma_x^2))exp[-(4pi^2(mu_x-x)^22N)/(4·4pi^2sigma_x^2)]](https://mathworld.wolfram.com/images/equations/CentralLimitTheorem/Inline79.gif) |
(28) |
 |
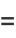 |
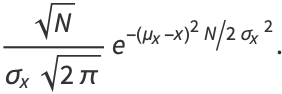 |
(29) |
But 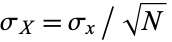 and
and 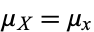 , so
, so
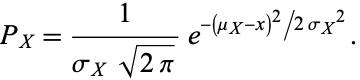 |
(30) |
The "fuzzy" central limit theorem says that data which are influenced by many small and unrelated random effects are approximately normally distributed.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 1972.
Feller, W. "The Fundamental Limit Theorems in Probability." Bull. Amer. Math. Soc. 51, 800-832, 1945.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, p. 229, 1968.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 2, 3rd ed. New York: Wiley, 1971.
Kallenberg, O. Foundations of Modern Probability. New York: Springer-Verlag, 1997.
Lindeberg, J. W. "Eine neue Herleitung des Exponentialgesetzes in der Wahrscheinlichkeitsrechnung." Math. Z. 15, 211-225, 1922.
Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, pp. 112-113, 1992.
Trotter, H. F. "An Elementary Proof of the Central Limit Theorem." Arch. Math. 10, 226-234, 1959.
Zabell, S. L. "Alan Turing and the Central Limit Theorem." Amer. Math. Monthly 102, 483-494, 1995.



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
لحماية التراث الوطني.. العتبة العباسية تعلن عن ترميم أكثر من 200 وثيقة خلال عام 2024
|
|
|