المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Noncentral Student,s t-Distribution |
 1821
 03:26 مساءً
date: 10-4-2021 |
Author : المرجع الالكتروني للمعلوماتيه 
Book or Source : www.almerja.com 
Page and Part : ...|
Read More
Date: 2-5-2021
2071
Date: 7-2-2021
1645
Date: 1-4-2021
3709
|
A generalization of Student's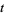 
-distribution known as the noncentral Student's 
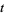-distribution is given by
![P(x)=(n^(n/2)n!)/(2^ne^(lambda^2/2)(n+x^2)^(n/2)Gamma(1/2n)){(sqrt(2)lambdax_1F_1(1/2n+1;3/2;(lambda^2x^2)/(2(n+x^2))))/((n+x^2)Gamma[1/2(n+1)])+(_1F_1(1/2(n+1);1/2;(lambda^2x^2)/(2(n+x^2))))/(sqrt(n+x^2)Gamma(1/2n+1))},](https://mathworld.wolfram.com/images/equations/NoncentralStudentst-Distribution/NumberedEquation1.gif) |
(1) |
where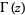 
is the gamma function and 
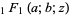is a confluent hypergeometric function of the first kind.
This distribution is implemented in the Wolfram Language as NoncentralStudentTDistribution[n, lambda].
The mean and variance are given by
 |
 |
 |
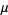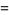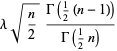(2) |
 |
 |
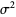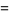![((lambda^2+1)n)/(n-2)-(lambda^2n[Gamma(1/2(n-1))]^2)/(2[Gamma(1/2n)]^2).](https://mathworld.wolfram.com/images/equations/NoncentralStudentst-Distribution/Inline10.gif) |
|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
ضمن مؤتمر ذاكرة الألم في العراق باحث يتطرّق إلى استراتيجية كرسي اليونسكو في دراسات منع الإبادة الجماعية في العالم الإسلامي
|
|
|
