Moore-Penrose Matrix Inverse

Given an 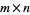 matrix 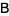, the Moore-Penrose generalized matrix inverse is a unique  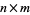matrix pseudoinverse 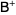. This matrix was independently defined by Moore in 1920 and Penrose (1955), and variously known as the generalized inverse, pseudoinverse, or Moore-Penrose inverse. It is a matrix 1-inverse, and is implemented in the Wolfram Language as PseudoInverse[m].

The Moore-Penrose inverse satisfies

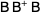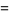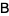			(1)
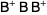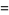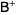			(2)
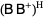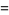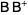			(3)
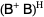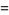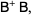			(4)

where 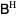 is the conjugate transpose.

It is also true that

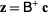(5)

is the shortest length least squares solution to the problem

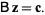(6)

If the inverse of 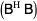 exists, then

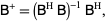(7)

as can be seen by premultiplying both sides of (6) by 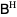 to create a square matrix which can then be inverted,

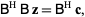(8)

giving

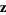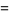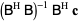			(9)
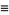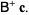			(10)

REFERENCES:

Ben-Israel, A. and Greville, T. N. E. Generalized Inverses: Theory and Applications. New York: Wiley, 1977.

Campbell, S. L. and Meyer, C. D. Jr. Generalized Inverses of Linear Transformations. New York: Dover, 1991.

Lawson, C. and Hanson, R. Solving Least Squares Problems. Englewood Cliffs, NJ: Prentice-Hall, 1974.

Penrose, R. "A Generalized Inverse for Matrices." Proc. Cambridge Phil. Soc. 51, 406-413, 1955.

Rao, C. R. and Mitra, S. K. Generalized Inverse of Matrices and Its Applications. New York: Wiley, 1971.