


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 31-10-2019
Date: 19-9-2020
Date: 10-2-2020
|
For an integer 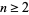 , let
, let 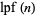 denote the least prime factor of
denote the least prime factor of 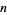 . A pair of integers
. A pair of integers 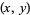 is called a twin peak if
is called a twin peak if
1. 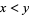 ,
,
2. 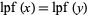 ,
,
3. For all  ,
, 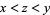 implies
implies 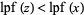 .
.
A broken-line graph of the least prime factor function resembles a jagged terrain of mountains. In terms of this terrain, a twin peak consists of two mountains of equal height with no mountain of equal or greater height between them. Denote the height of twin peak  by
by 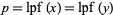 . By definition of the least prime factor function,
. By definition of the least prime factor function, 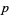 must be prime.
must be prime.
Call the distance between two twin peaks 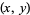
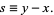 |
(1) |
Then 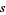 must be an even multiple of
must be an even multiple of 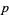 ; that is,
; that is, 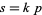 where
where 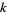 is even. A twin peak with
is even. A twin peak with 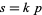 is called a
is called a 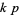 -twin peak. Thus we can speak of
-twin peak. Thus we can speak of 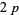 -twin peaks,
-twin peaks, 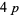 -twin peaks, etc. A
-twin peaks, etc. A 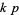 -twin peak is fully specified by
-twin peak is fully specified by 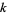 ,
, 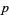 , and
, and  , from which we can easily compute
, from which we can easily compute 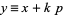 .
.
The set of 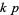 -twin peaks is periodic with period
-twin peaks is periodic with period 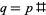 , where
, where 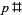 is the primorial of
is the primorial of 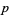 . That is, if
. That is, if 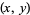 is a
is a 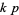 -twin peak, then so is
-twin peak, then so is 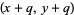 . A fundamental
. A fundamental 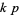 -twin peak is a twin peak having
-twin peak is a twin peak having  in the fundamental period
in the fundamental period 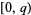 . The set of fundamental
. The set of fundamental 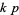 -twin peaks is symmetric with respect to the fundamental period; that is, if
-twin peaks is symmetric with respect to the fundamental period; that is, if 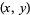 is a twin peak on
is a twin peak on 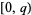 , then so is
, then so is 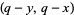 .
.
The question of the existence of twin peaks was first raised by David Wilson (pers. comm., Feb. 10, 1997). Wilson already had privately showed the existence of twin peaks of height 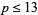 to be unlikely, but was unable to rule them out altogether. Later that same day, John H. Conway, Johan de Jong, Derek Smith, and Manjul Bhargava collaborated to discover the first twin peak. Two hours at the blackboard revealed that
to be unlikely, but was unable to rule them out altogether. Later that same day, John H. Conway, Johan de Jong, Derek Smith, and Manjul Bhargava collaborated to discover the first twin peak. Two hours at the blackboard revealed that 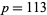 admits the
admits the 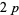 -twin peak
-twin peak
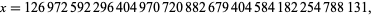 |
(2) |
which settled the existence question. Immediately thereafter, Fred Helenius found the smaller 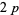 -twin peak with
-twin peak with 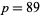 and
and
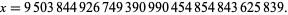 |
(3) |
The effort now shifted to finding the least prime 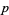 admitting a
admitting a 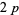 -twin peak. On Feb. 12, 1997, Fred Helenius found
-twin peak. On Feb. 12, 1997, Fred Helenius found 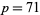 , which admits 240 fundamental
, which admits 240 fundamental 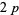 -twin peaks, the least being
-twin peaks, the least being
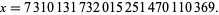 |
(4) |
Helenius's results were confirmed by Dan Hoey, who also computed the least 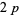 -twin peak
-twin peak 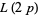 and number of fundamental
and number of fundamental 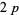 -twin peaks
-twin peaks 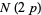 for
for 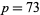 , 79, and 83. His results are summarized in the following table (OEIS A009190).
, 79, and 83. His results are summarized in the following table (OEIS A009190).
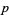 |
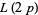 |
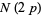 |
| 71 | 7310131732015251470110369 | 240 |
| 73 | 2061519317176132799110061 | 40296 |
| 79 | 3756800873017263196139951 | 164440 |
| 83 | 6316254452384500173544921 | 6625240 |
The 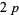 -twin peak of height
-twin peak of height 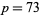 is the smallest known twin peak. Wilson found the smallest known
is the smallest known twin peak. Wilson found the smallest known 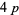 -twin peak with
-twin peak with 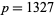 , as well as another very large
, as well as another very large 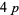 -twin peak with
-twin peak with 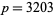 . Richard Schroeppel noted that the latter twin peak is at the high end of its fundamental period and that its reflection within the fundamental period
. Richard Schroeppel noted that the latter twin peak is at the high end of its fundamental period and that its reflection within the fundamental period 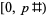 is smaller.
is smaller.
Many open questions remain concerning twin peaks, e.g.,
1. What is the smallest twin peak (smallest 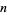 )?
)?
2. What is the least prime 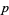 admitting a
admitting a 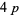 -twin peak?
-twin peak?
3. Do 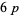 -twin peaks exist?
-twin peaks exist?
4. Is there, as Conway has argued, an upper bound on the span of twin peaks?
5. Let 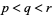 be prime. If
be prime. If 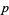 and
and 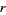 each admit
each admit 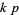 -twin peaks, does
-twin peaks, does 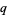 then necessarily admit a
then necessarily admit a 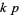 -twin peak?
-twin peak?
REFERENCES:
Sloane, N. J. A. Sequence A009190 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|