التركيب الدوراني للحزم الالكترونية

يحتوي كل انتقال اهتزازي لحزمة الكترونية تركيبا دقيقا نظرا للتغير في طاقة الجزيئة الدورانية المصاحب للانتقال الاهتزازي – الالكتروني مكونا حزمة ثانوية داخل الحزمة الالكترونية.

وباعتماد نموذج الدوار الصلد يمكن التعبير عن تركيب الحزمة الثانوية بالمعادلة:

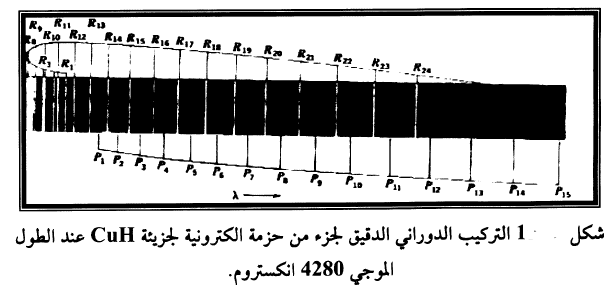
.......(1)

حيث ^'B_v و^"B_v الثوابت الدورانية للحالات الاهتزازية والالكترونية المتضمنة في الانتقال و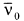 يمثل انتقال اهتزازي معين لانتقال الكتروني بوحدات cm^-1 عندما J'= J"=0 ويدعى اصل الحزمة.

وفي حالة انتقالات Σ-Σ​ توجد خطوط (ΔJ = -1) او خطوط ΔJ = +1)R) فقط بينما الانتقالات Σ-Π​ او Π-Π توجد خطوط ΔJ = 0)Q) ايضا ومن المعادلة (1) نحصل على:

خطوط P       J"= J, J'= J-1

خطوط Q        J"= J, J'= J

خطوط R      J"= J, J'= J+1

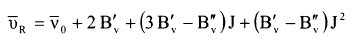
والاختلاف الاساسي في تحليل التركيب الدوراني للانتقالات الاهتزازية – الالكترونية هو ان ^'B_v و^"B_v يمكن ان تكون مختلفة جدا لحالات الجزيئة الالكترونية المختلفة ويصبح مكافئ الحد J² كبيرا وبذلك لن تتحرك مكونات الفرع P والفرع R خطيا مبتعدة عن اصل الحزمة.

فمثلا اذا كان ^'B_v" < B_v فإن حدود J² لفرع P تصبح اكبر بالمقدار من الحدود الخطية في J وستتحرك مكونات الفرع الى الترددات الاعلى بدلا من الترددات الاوطأ مع زيادة في J وبالمثل اذا كان ^'B_v" > B_v فان حدود J² لفرع Q يصبح مقدارها اكبر من الحدود الخطية في J وستتحرك مركبات J في الحزمة الى الترددات الاوطأ بدلا من الترددات الاعلى مع زيادة J ويؤدي ذلك الى تكوين راس الحزمة في التركيب الدوراني في كل حزمة اهتزازية ثانوية لحزمة الكترونية معينة.

وفي شكل (1) مبين انتقال الكتروني لجزيئة CuH بقاعدة اختيار -+ = ΔJ وفيه موضح تكوين راس الحزمة والعودة الى الخلف وبرسم ترددات الخطوط ضد العدد الكمي نحصل على قطع مكافئ كما هو مبين في شكل (2a) و (2b) ويدعى قطع مكافئ فورترات Fortrat parabola.

ان تحليل تركيب الفروع الدورانية يؤدي الى الحصول على الثوابت الدورانية 'B_v و"B_v لحلالتين المتضمنتين في الانتقال وبهذه الطريقة يمكن الحصول على معلومات عن طول الاصرة في حالة الاتزان للحالة الارضية والحالة المتهيجة.

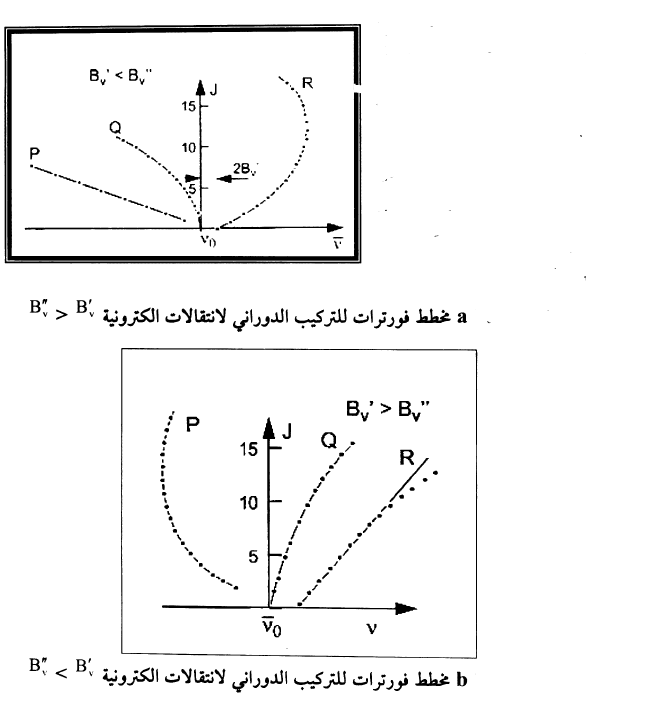
شكل (2)

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد

مواضيع ذات صلة

الكشف عن الألغام والمتفجرات

الكربون .. أمير المواد وعميدها

خواص المواد النانوية

تاريخ أنابيب الكربون النانوية (History of carbon nanotubes)

الاتصال والحوار العام في تطوير تقنية النانو

نشاطات المنظمات الدولية في مجال التقنية النانوية

حالة المعارف المتصلة بمخاطر المواد النانوية

الاعتبارات الأخلاقية في التقنية النانويه

المنفعة الاجتماعية للتقنية النانوية

ما المقصود بالنانو؟

النانو تكنولوجيا.. علم وصناعة القرن الجديد

أنابيب الكربون النانوية Nanotubes Carbon