


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 6-12-2020
Date: 14-11-2019
Date: 8-5-2020
|
The abundance of a number 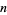 , sometimes also called the abundancy (a term which in this work, is reserved for a different but related quantity), is the quantity
, sometimes also called the abundancy (a term which in this work, is reserved for a different but related quantity), is the quantity
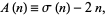 |
where 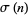 is the divisor function. The abundances of
is the divisor function. The abundances of  , 2, ... are
, 2, ... are 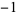 ,
, 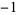 ,
, 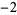 ,
, 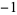 ,
, 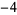 , 0,
, 0, 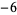 ,
, 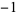 ,
, 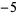 ,
, 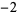 ,
, 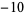 , 4,
, 4, 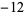 ,
, 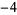 ,
, 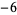 ,
, 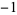 , ... (OEIS A033880).
, ... (OEIS A033880).
The following table lists special classifications given to a number 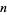 based on the value of
based on the value of 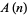 .
.
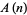 |
class | OEIS | list of 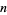 |
 |
deficient number | A005100 | 1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17, ... |
 |
almost perfect number | A000079 | 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, ... |
| 0 | perfect number | A000396 | 6, 28, 496, 8128, ... |
| 1 | quasiperfect number | none known | |
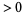 |
abundant number | A005101 | 12, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, ... |
Values of 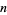 such that
such that 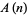 is odd are given by
is odd are given by 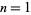 , 2, 4, 8, 9, 16, 18, 25, 32, ... (OEIS A028982; i.e., the union of nonzero squares and twice the squares). Values of
, 2, 4, 8, 9, 16, 18, 25, 32, ... (OEIS A028982; i.e., the union of nonzero squares and twice the squares). Values of 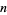 such that
such that 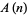 is square are given by
is square are given by 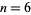 , 12, 28, 70, 88, 108, 168, ... (OEIS A109510).
, 12, 28, 70, 88, 108, 168, ... (OEIS A109510).
REFERENCES:
Guy, R. K. Unsolved Problems in Number Theory, 3rd ed. New York: Springer-Verlag, 2004.
Sloane, N. J. A. Sequences A000079/M1129, A000396/M4186, A005100/M0514, A005101/M4825, A028982, A033880, and A109510 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|