


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-3-2020
Date: 14-8-2020
Date: 27-8-2020
|
Consider the sequence 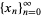 defined by
defined by 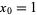 and
and
![x_(n+1)=[3/2x_n],](https://mathworld.wolfram.com/images/equations/PowerCeilings/NumberedEquation1.gif) |
where ![[z]](https://mathworld.wolfram.com/images/equations/PowerCeilings/Inline3.gif) is the ceiling function. For
is the ceiling function. For 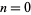 , 1, ..., the first few terms are 1, 2, 3, 5, 8, 12, 18, 27, 41, 62, ... (OEIS A061419; Wolfram 2002, p. 100, Fig. (b)).
, 1, ..., the first few terms are 1, 2, 3, 5, 8, 12, 18, 27, 41, 62, ... (OEIS A061419; Wolfram 2002, p. 100, Fig. (b)).
Odlyzko and Wilf (1991) have shown that 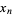 satisfies
satisfies
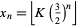 |
for all 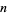 , where
, where 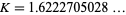 (OEIS A083286) is analogous to Mills' constant in the sense that the formula is useless unless
(OEIS A083286) is analogous to Mills' constant in the sense that the formula is useless unless 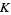 is known exactly ahead of time (Odlyzko and Wilf 1991, Finch 2003).
is known exactly ahead of time (Odlyzko and Wilf 1991, Finch 2003).
REFERENCES:
Finch, S. R. "Powers of 3/2 Modulo One." §2.30.1 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 194-199, 2003.
Odlyzko, A. M. and Wilf, H. S. "Functional Iteration and the Josephus Problem." Glasgow Math. J. 33, 235-240, 1991.
Sloane, N. J. A. Sequences A061419 and A083286 in "The On-Line Encyclopedia of Integer Sequences."
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 100, 2002.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
ضمن مؤتمر ذاكرة الألم في العراق مدير كرسي اليونسكو في جامعة الموصل يقدّم دراسةً تناقش استراتيجية الكرسي لنبذ التطرف وتعزيز ثقافة السلام
|
|
|