
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
SINE WAVES AS CIRCULAR MOTION
المؤلف:
S. Gibilisco
المصدر:
Physics Demystified
الجزء والصفحة:
329
5-10-2020
2398
SINE WAVES AS CIRCULAR MOTION
Suppose that you swing a glowing ball around and around at the end of a string at a rate of one revolution per second. The ball thus describes a circle in space (Fig. 1a). Imagine that you swing the ball around so that it is always at the same level; it takes a path that lies in a horizontal plane. Imagine that you do this in a pitch-dark gymnasium. If a friend stands some distance away with his or her eyes in the plane of the ball’s path, what does your friend see? Only the glowing ball, oscillating back and forth. The ball seems to move toward the right, slow down, and then reverse its direction,

Fig. 1. Swinging ball and string. (a) as seen from above; (b) as seen from some distance away in the plane of the ball’s circular path.
going back toward the left (see Fig. 1b). Then it moves faster and faster and then slower again, reaching its left-most point, at which it turns around again. This goes on and on, with a frequency of 1 Hz, or a complete cycle per second, because you are swinging the ball around at one revolution per second.
If you graph the position of the ball as seen by your friend with respect to time, the result will be a sine wave (Fig. 2). This wave has the same characteristic shape as all sine waves. The standard, or basic, sine wave is described by the mathematical function y=sin x in the (x, y) coordinate plane. The general form is y = a sin bx, where a and b are real-number constants.
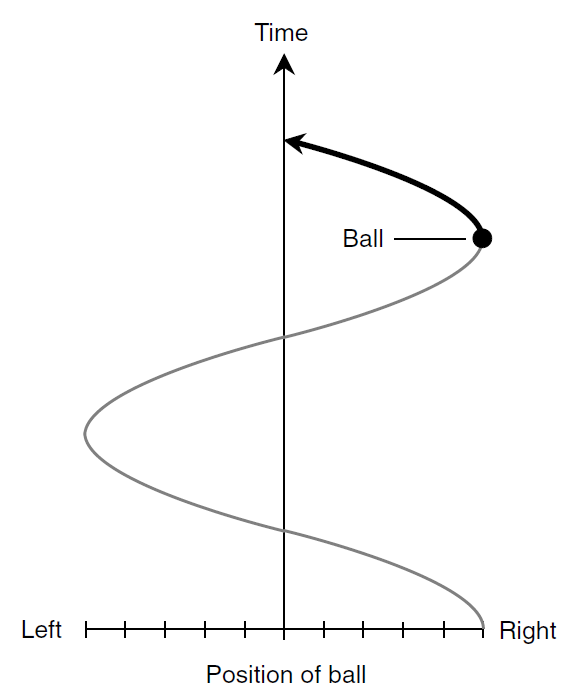
Fig. 2. Position of ball as seen edge-on as a function of time.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















