


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-1-2021
Date: 2-2-2016
Date: 13-1-2021
|
A number 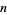 with prime factorization
with prime factorization
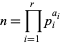 |
is called 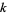 -almost prime if it has a sum of exponents
-almost prime if it has a sum of exponents 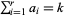 , i.e., when the prime factor (multiprimality) function
, i.e., when the prime factor (multiprimality) function 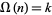 .
.
The set of 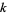 -almost primes is denoted
-almost primes is denoted 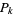 .
.
The primes correspond to the "1-almost prime" numbers and the 2-almost prime numbers correspond to semiprimes. Conway et al. (2008) propose calling these numbers primes, biprimes, triprimes, and so on.
Formulas for the number of 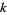 -almost primes less than or equal to
-almost primes less than or equal to 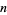 are given by
are given by
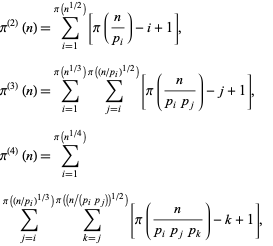 |
and so on, where 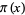 is the prime counting function and
is the prime counting function and 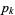 is the
is the 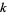 th prime (R. G. Wilson V, pers. comm., Feb. 7, 2006; the first of which was discovered independently by E. Noel and G. Panos around Jan. 2005, pers. comm., Jun. 13, 2006).
th prime (R. G. Wilson V, pers. comm., Feb. 7, 2006; the first of which was discovered independently by E. Noel and G. Panos around Jan. 2005, pers. comm., Jun. 13, 2006).
The following table summarizes the first few 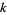 -almost primes for small
-almost primes for small 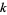 .
.
 |
OEIS | 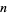 -almost primes -almost primes |
| 1 | A000040 | 2, 3, 5, 7, 11, 13, ... |
| 2 | A001358 | 4, 6, 9, 10, 14, 15, 21, 22, ... |
| 3 | A014612 | 8, 12, 18, 20, 27, 28, 30, 42, 44, 45, 50, 52, ... |
| 4 | A014613 | 16, 24, 36, 40, 54, 56, 60, 81, 84, 88, 90, 100, ... |
| 5 | A014614 | 32, 48, 72, 80, 108, 112, 120, 162, 168, 176, 180, ... |
REFERENCES:
Conway, J. H.; Dietrich, H.; O'Brien, E. A. "Counting Groups: Gnus, Moas, and Other Exotica." Math. Intell. 30, 6-18, 2008.
Sloane, N. J. A. Sequences A000040/M0652, A001358/M3274, A014612, A014613, and A014614 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
عوائل الشهداء: العتبة العباسية المقدسة سبّاقة في استذكار شهداء العراق عبر فعالياتها وأنشطتها المختلفة
|
|
|