


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-3-2020
Date: 10-10-2020
Date: 8-7-2020
|
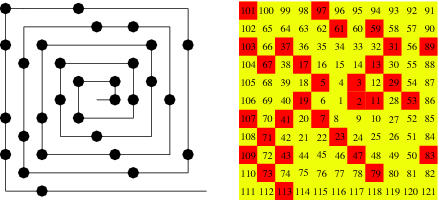
The prime spiral, also known as Ulam's spiral, is a plot in which the positive integers are arranged in a spiral (left figure), with primes indicated in some way along the spiral. In the right plot above, primes are indicated in red and composites are indicated in yellow.

The plot above shows a larger part of the spiral in which the primes are shown as dots.

Unexpected patterns of diagonal lines are apparent in such a plot, as illustrated in the above  grid. This construction was first made by Polish-American mathematician Stanislaw Ulam (1909-1986) in 1963 while doodling during a boring talk at a scientific meeting. While drawing a grid of lines, he decided to number the intersections according to a spiral pattern, and then began circling the numbers in the spiral that were primes. Surprisingly, the circled primes appeared to fall along a number of diagonal straight lines or, in Ulam's slightly more formal prose, it "appears to exhibit a strongly nonrandom appearance" (Stein et al. 1964). The spiral appeared on the March 1964 cover of Scientific American magazine.
grid. This construction was first made by Polish-American mathematician Stanislaw Ulam (1909-1986) in 1963 while doodling during a boring talk at a scientific meeting. While drawing a grid of lines, he decided to number the intersections according to a spiral pattern, and then began circling the numbers in the spiral that were primes. Surprisingly, the circled primes appeared to fall along a number of diagonal straight lines or, in Ulam's slightly more formal prose, it "appears to exhibit a strongly nonrandom appearance" (Stein et al. 1964). The spiral appeared on the March 1964 cover of Scientific American magazine.
Remarkably, noted science fiction author Arthur C. Clarke described the prime spiral in his novel The City and the Stars (1956, Ch. 6, p. 54). Clarke wrote, "Jeserac sat motionless within a whirlpool of numbers. The first thousand primes.... Jeserac was no mathematician, though sometimes he liked to believe he was. All he could do was to search among the infinite array of primes for special relationships and rules which more talented men might incorporate in general laws. He could find how numbers behaved, but he could not explain why. It was his pleasure to hack his way through the arithmetical jungle, and sometimes he discovered wonders that more skillful explorers had missed. He set up the matrix of all possible integers, and started his computer stringing the primes across its surface as beads might be arranged at the intersections of a mesh."
However, Clarke never actually performed this thought experiment (pers. comm. to E. Pegg Jr., May 27, 2002), thus leaving discovery of the unexpected properties of the prime spiral to Ulam seven years later.
M. Charpentier has written a PostScript file which can be downloaded to a printer and draws a prime spiral.

A hexagonal prime spiral can also be constructed, as illustrated above (Abbott 2005).
REFERENCES:
Abbott, P. (Ed.). "Mathematica One-Liners: Spiral on an Integer Lattice." Mathematica J. 1, 39, 1990.
Abbott, P. "Re: Hexagonal Spiral." https://forums.wolfram.com/mathgroup/archive/2005/May/msg00336.html. May 11, 2005.
Charpentier, M. "Prime Numbers in PostScript." https://www.cs.unh.edu/~charpov/Programming/PostScript-primes/.
Clarke, A. C. The City and the Stars. New York: Harcourt, Brace, 1956.
Dewdney, A. K. "Computer Recreations: How to Pan for Primes in Numerical Gravel." Sci. Amer. 259, 120-123, July 1988.
Ellerstein, S. M. "The Pronic Renaissance: The Ulam Square Spiral (Modified)." J. Recr. Math. 29, 188-189, 1998.
Gardner, M. "Mathematical Recreations: The Remarkable Lore of the Prime Number." Sci. Amer. 210, 120-128, Mar. 1964.
Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, pp. 80-83 and 88-89, 1984.
Goddard, T. "Ulam Spiral." https://d4maths.lowtech.org/mirage/ulam.htm.
Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, pp. 105-109, 1998.
Lane, C. "Prime Spiral." https://cdl.best.vwh.net/Java/PrimeSpiralApplet.html.
Leatherland, A. J. F. "The Mysterious Prime Spiral Phenomenon." https://yoyo.cc.monash.edu.au/~bunyip/primes/#spiral.
Morin, D. "Le Village Premier." https://platon.lacitec.on.ca/~dmorin/applet/village/.
Peterson, I. "MathTrek: Prime Spirals." May 4, 2002. https://www.sciencenews.org/20020504/mathtrek.asp.
Pickover, C. "A Prime Plaid." In Computers and the Imagination: Visual Adventures Beyond the Edge. New York: St. Martin's, 1991.
Stein, M. and Ulam, S. M. "An Observation on the Distribution of Primes." Amer. Math. Monthly 74, 43-44, 1967.
Stein, M. L.; Ulam, S. M.; and Wells, M. B. "A Visual Display of Some Properties of the Distribution of Primes." Amer. Math. Monthly 71, 516-520, 1964.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|