Connell Sequence

The Connell sequence is the sequence obtained by starting with the first positive odd number (1), taking the next two even numbers (2, 4), the next three odd numbers (5, 7, 9), the next four even numbers (10, 12, 14, 16), and so on. The first few terms are 1, 2, 4, 5, 7, 9, 10, 12, 14, 16, 17, ... (OEIS A001614). A binary plot of the sequence from 1 to 255 is illustrated above.

Amazingly, the terms of this sequence have the closed form

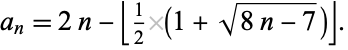This shows immediately that

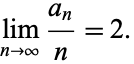REFERENCES:

Connell, I. "Elementary Problem E1382." Amer. Math. Monthly 66, 724, 1959.

Connell, I. "An Unusual Sequence." Amer. Math. Monthly 67, 380, 1960.

Iannucci, D. E. and Mills-Taylor, D. "On Generalizing the Connell Sequence." J. Integer Sequences 2, No. 99.1.7, 1999. https://www.cs.uwaterloo.ca/journals/JIS/.

Lakhtakia, A. and Pickover, C. "The Connell Sequence." J. Recr. Math. 25, 90-92, 1993.

Pickover, C. A. Computers and the Imagination. New York: St. Martin's Press, p. 276, 1991.

Pickover, C. A. "Bird, Dog Dog, Bird, Bird Bird, Dog Dog Dog Dog." Ch. 39 in The Mathematics of Oz: Mental Gymnastics from Beyond the Edge. New York: Cambridge University Press, pp. 88-89 and 294-295, 2002.

Sloane, N. J. A. Sequence A001614/M0962 in "The On-Line Encyclopedia of Integer Sequences."

Stevens, G. E. "A Connell-Like Sequence." J. Integer Sequences 1, Np. 98.1.4, 1998. https://www.cs.uwaterloo.ca/journals/JIS/.