


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 31-8-2020
Date: 24-11-2020
Date: 10-3-2020
|
An irrational number  can be called GK-regular (defined here for the first time) if the distribution of its continued fraction coefficients is the Gauss-Kuzmin distribution. An irrational number that is not GK-regular is said to be GK-irregular. It has been shown that all real numbers except for a set of measure zero are GK-regular.
can be called GK-regular (defined here for the first time) if the distribution of its continued fraction coefficients is the Gauss-Kuzmin distribution. An irrational number that is not GK-regular is said to be GK-irregular. It has been shown that all real numbers except for a set of measure zero are GK-regular.
Classes of GK-irregular numbers include rational and real quadratic numbers and numbers of the form 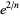 where
where 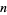 is a nonzero integer. Most widely-studied real numbers not of one of these forms, such as
is a nonzero integer. Most widely-studied real numbers not of one of these forms, such as 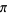 and algebraic numbers of degree greater than 2, are strongly suspected to be GK-regular based on numerical evidence, although no proof is known. The situation is much the same for normal and absolutely normal numbers.
and algebraic numbers of degree greater than 2, are strongly suspected to be GK-regular based on numerical evidence, although no proof is known. The situation is much the same for normal and absolutely normal numbers.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|