


 علم الكيمياء
علم الكيمياء 
 الكيمياء التحليلية
الكيمياء التحليلية 
 الكيمياء الحياتية
الكيمياء الحياتية 
 الكيمياء العضوية
الكيمياء العضوية 
 الكيمياء الفيزيائية
الكيمياء الفيزيائية
 الكيمياء اللاعضوية
الكيمياء اللاعضوية 
 مواضيع اخرى في الكيمياء
مواضيع اخرى في الكيمياء
 الكيمياء الصناعية
الكيمياء الصناعية |
Read More
Date: 30-4-2020
Date: 2-5-2020
Date: 28-4-2020
|
In order to keep this lesson within reasonable bounds, we are limiting it mostly to crystals belonging to the so-called cubic system. In doing so, we can develop the major concepts that are useful for understanding more complicated structures (as if there are not enough complications in cubics alone!) But in addition, it happens that cubic crystals are very commonly encountered; most metallic elements have cubic structures, and so does ordinary salt, sodium chloride.
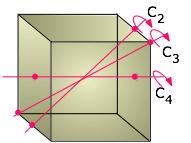
We usually think of a cubic shape in terms of the equality of its edge lengths and the 90° angles between its sides, but there is another way of classifying shapes that chemists find very useful. This is to look at what geometric transformations (such as rotations around an axis) we can perform that leave the appearance unchanged. For example, you can rotate a cube 90° around an axis perpendicular to any pair of its six faces without making any apparent change to it. We say that the cube possesses three mutually perpendicular four-fold rotational axes, abbreviated C4 axes. But if you think about it, a cube can also be rotated around the axes that extend between opposite corners; in this case, it takes three 120° rotations to go through a complete circle, so these axes (also four in number) are three-fold or C3 axes.
Cubic crystals belong to one of the seven crystal systems whose lattice points can be extended indefinitely to fill three-dimensional space and which can be constructed by successive translations (movements) of a primitive unit cell in three dimensions. As we will see below, the cubic system, as well as some of the others, can have variants in which additional lattice points can be placed at the center of the unit or at the center of each face.


|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
تضاريس شبيهة بـ"الجبنة السويسرية".. حفرة غامضة على المريخ
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|