


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-5-2020
Date: 5-12-2020
Date: 20-9-2020
|
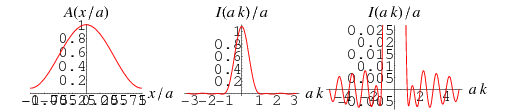
An apodization function chosen to minimize the height of the highest sidelobe (Hamming and Tukey 1949, Blackman and Tukey 1959). The Hamming function is given by
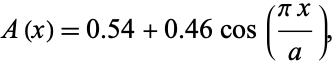 |
(1) |
and its full width at half maximum is 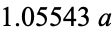 .
.
The corresponding instrument function is
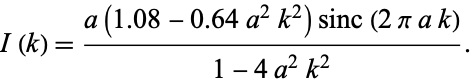 |
(2) |
This apodization function is close to the one produced by the requirement that the instrument function goes to 0 at 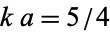 . The FWHM is
. The FWHM is 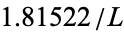 , the peak is 1.08, and the peak negative and positive sidelobes (in units of the peak) are
, the peak is 1.08, and the peak negative and positive sidelobes (in units of the peak) are 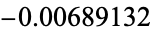 and 0.00734934, respectively.
and 0.00734934, respectively.
From the apodization function, a general symmetric apodization function 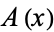 can be written as a Fourier series
can be written as a Fourier series
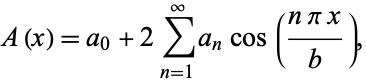 |
(3) |
where the coefficients satisfy
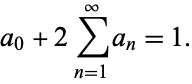 |
(4) |
The corresponding instrument function is
![I(t)=2b{a_0sinc(2pikb)+sum_(n=1)^infty[sinc(2pikb+npi)+sinc(2pikb-npi)]}.](https://mathworld.wolfram.com/images/equations/HammingFunction/NumberedEquation5.gif) |
(5) |
To obtain an apodization function with zero at 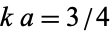 , use
, use
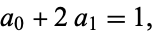 |
(6) |
so
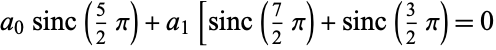 |
(7) |
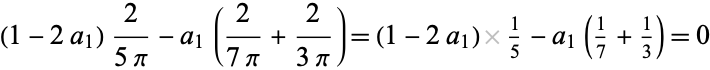 |
(8) |
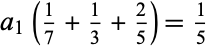 |
(9) |
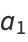 |
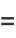 |
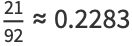 |
(10) |
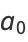 |
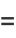 |
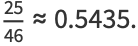 |
(11) |
REFERENCES:
Blackman, R. B. and Tukey, J. W. "Particular Pairs of Windows." In The Measurement of Power Spectra, From the Point of View of Communications Engineering. New York: Dover, pp. 98-99, 1959.
Hamming, R. W. and Tukey, J. W. "Measuring Noise Color." Unpublished memorandum, 1949.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|