


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-2-2020
Date: 24-10-2020
Date: 24-12-2019
|
Let 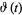 be the Riemann-Siegel function. The unique value
be the Riemann-Siegel function. The unique value 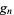 such that
such that
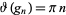 |
(1) |
where 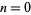 , 1, ... is then known as a Gram point (Edwards 2001, pp. 125-126).
, 1, ... is then known as a Gram point (Edwards 2001, pp. 125-126).
An excellent approximation for Gram point 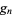 can be obtained by using the first few terms in the asymptotic expansion for
can be obtained by using the first few terms in the asymptotic expansion for 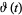 and inverting to obtain
and inverting to obtain
![g_n approx 2piexp[1+W((8n+1)/(8e))],](https://mathworld.wolfram.com/images/equations/GramPoint/NumberedEquation2.gif) |
(2) |
where 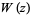 is the Lambert W-function. This approximation gives as error of
is the Lambert W-function. This approximation gives as error of 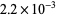 for
for 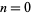 , decreasing to
, decreasing to 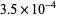 by
by 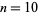 .
.
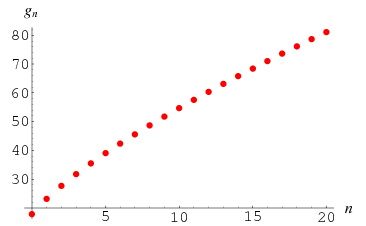
The following table gives the first few Gram points.
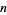 |
OEIS | 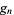 |
| 0 | A114857 | 17.8455995404 |
| 1 | A114858 | 23.1702827012 |
| 2 | 27.6701822178 | |
| 3 | 31.7179799547 | |
| 4 | 35.4671842971 | |
| 5 | 38.9992099640 | |
| 6 | 42.3635503920 | |
| 7 | 45.5930289815 | |
| 8 | 48.7107766217 | |
| 9 | 51.7338428133 | |
| 10 | 54.6752374468 |
The integers closest to these points are 18, 23, 28, 32, 35, 39, 42, 46, 49, 52, 55, 58, ... (OEIS A002505).
There is a unique point at which 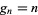 , given by the solution to the equation
, given by the solution to the equation
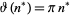 |
(3) |
and having numerical value
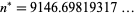 |
(4) |
(OEIS A114893).
It is usually the case that ![R[zeta(1/2+ig_n)]=(-1)^nZ(g_n)>0](https://mathworld.wolfram.com/images/equations/GramPoint/Inline14.gif) . Values of
. Values of 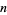 for which this does not hold are
for which this does not hold are 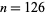 , 134, 195, 211, 232, 254, 288, ... (OEIS A114856), the first two of which were found by Hutchinson (1925).
, 134, 195, 211, 232, 254, 288, ... (OEIS A114856), the first two of which were found by Hutchinson (1925).
REFERENCES:
Edwards, H. M. Riemann's Zeta Function. New York: Dover, 2001.
Gram, J.-P. "Sur les zéros de la fonction 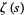 de Riemann." Acta Math. 27, 289-304, 1903.
de Riemann." Acta Math. 27, 289-304, 1903.
Haselgrove, C. B. and Miller, J. C. P. "Tables of the Riemann Zeta Function." Royal Society Mathematical Tables, Vol. 6. Cambridge, England: Cambridge University Press, p. 58, 1960.
Hutchinson, J. I. "On the Roots of the Riemann Zeta-Function." Trans. Amer. Math. Soc. 27, 49-60, 1925.
Sloane, N. J. A. Sequences A002505/M5052, A114856, A114857, A114858, and A114893 Sloane, N. J. A. Sequences



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|