


 علم الكيمياء
علم الكيمياء 
 الكيمياء التحليلية
الكيمياء التحليلية 
 الكيمياء الحياتية
الكيمياء الحياتية 
 الكيمياء العضوية
الكيمياء العضوية 
 الكيمياء الفيزيائية
الكيمياء الفيزيائية
 الكيمياء اللاعضوية
الكيمياء اللاعضوية 
 مواضيع اخرى في الكيمياء
مواضيع اخرى في الكيمياء
 الكيمياء الصناعية
الكيمياء الصناعية |
Read More
Date: 17-3-2020
Date: 4-2-2020
Date: 29-3-2020
|
To describe the periodic, three dimensional nature of crystals, the Laue equations are employed:
where a, b, and c are the three axes of the unit cell, θo, o, ?o are the angles of incident radiation, and ?, ?, ? are the angles of the diffracted radiation. A diffraction signal (constructive interference) will arise when h, k, and l are integer values. The rotating crystal method employs these equations. X-ray radiation is shown onto a crystal as it rotates around one of its unit cell axis. The beam strikes the crystal at a 90 degree angle. Using equation 1 above, we see that if θo is 90 degrees, then cosθo=0. For the equation to hold true, we can set h=0, granted that heta= 90. The above three equations will be satisfied at various points as the crystal rotates. This gives rise to a diffraction pattern (shown in the image below as multiple h values). The cylindrical film is then unwrapped and developed. The following equation can be used to determine the length axis around which the crystal was rotated:
where a is the length of the axis, y is the distance from h=0 to the h of interest, r is the radius of the firm, and ? is the wavelength of the x-ray radiation used. The first length can be determined with ease, but the other two require far more work, including remounting the crystal so that it rotates around that particular axis.
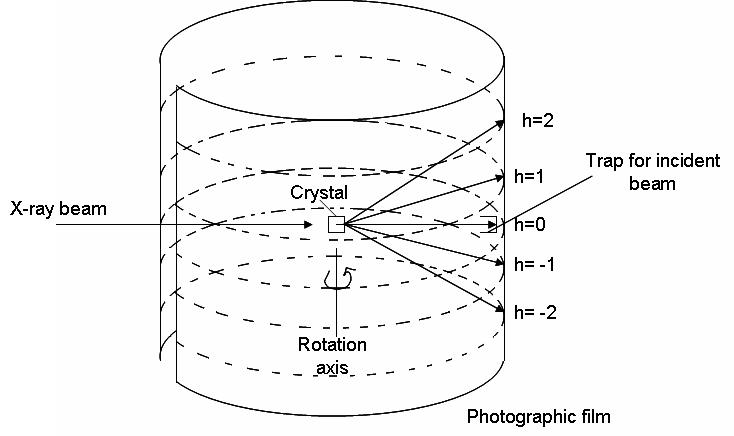
Figure 1:


|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
عوائل الشهداء: العتبة العباسية المقدسة سبّاقة في استذكار شهداء العراق عبر فعالياتها وأنشطتها المختلفة
|
|
|