


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-10-2019
Date: 28-9-2020
Date: 6-1-2021
|

Select three points at random on the circumference of a unit circle and find the distribution of areas of the resulting triangles determined by these three points.
The first point can be assigned coordinates 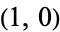 without loss of generality. Call the central angles from the first point to the second and third
without loss of generality. Call the central angles from the first point to the second and third 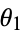 and
and 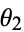 . The range of
. The range of 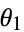 can be restricted to
can be restricted to ![[0,pi]](http://mathworld.wolfram.com/images/equations/CircleTrianglePicking/Inline5.gif) because of symmetry, but
because of symmetry, but 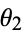 can range from
can range from 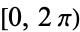 . Then
. Then
![A(theta_1,theta_2)=2sin(1/2theta_1)sin(1/2theta_2)sin[1/2(theta_1-theta_2)],](http://mathworld.wolfram.com/images/equations/CircleTrianglePicking/NumberedEquation1.gif) |
(1) |
so
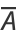 |
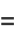 |
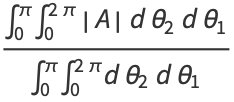 |
(2) |
 |
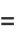 |
 |
(3) |
Therefore,
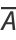 |
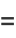 |
![2/(2pi^2)int_0^piint_0^(2pi)|sin(1/2theta_1)sin(1/2theta_2)sin[1/2(theta_1-theta_2)]|dtheta_2dtheta_1](http://mathworld.wolfram.com/images/equations/CircleTrianglePicking/Inline16.gif) |
(4) |
 |
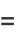 |
![1/(pi^2)int_0^pisin(1/2theta_1)[int_0^(2pi)sin(1/2theta_2)|sin[1/2(theta_2-theta_1)]|dtheta_2]dtheta_1](http://mathworld.wolfram.com/images/equations/CircleTrianglePicking/Inline19.gif) |
(5) |
 |
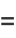 |
![1/(pi^2)int_0^(pi)int_0^(2pi); theta_2-theta_1>0sin(1/2theta_1)sin(1/2theta_2)sin[1/2(theta_1-theta_2)]dtheta_2dtheta_1+1/(pi^2)int_0^(pi)int_0^(2pi); theta_2-theta_1<0sin(1/2theta_1)sin(1/2theta_2)sin[1/2(theta_1-theta_2)]dtheta_2dtheta_1](http://mathworld.wolfram.com/images/equations/CircleTrianglePicking/Inline22.gif) |
(6) |
 |
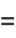 |
![1/(pi^2)int_0^pisin(1/2theta_1)[int_(theta_1)^(2pi)sin(1/2theta_2)sin[1/2(theta_2-theta_1)]dtheta_2]dtheta_1+1/(pi^2)int_0^pisin(1/2theta_1)[int_0^(theta_1)sin(1/2theta_2)sin[1/2(theta_2-theta_1)]dtheta_2]dtheta_1.](http://mathworld.wolfram.com/images/equations/CircleTrianglePicking/Inline25.gif) |
(7) |
But
![int(1/2theta_2)sin[1/2(theta_2-theta_1)]dtheta_2](http://mathworld.wolfram.com/images/equations/CircleTrianglePicking/Inline26.gif) |
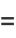 |
![intsin(1/2theta_2)[sin(1/2theta_2)cos(1/2theta_2)-sin(1/2theta_1)cos(1/2theta_2)]dtheta_2](http://mathworld.wolfram.com/images/equations/CircleTrianglePicking/Inline28.gif) |
(8) |
 |
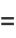 |
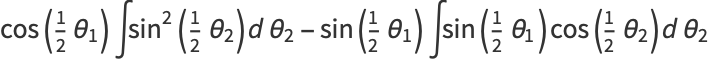 |
(9) |
 |
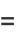 |
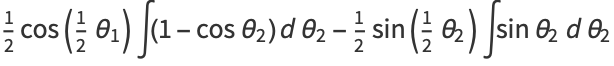 |
(10) |
 |
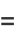 |
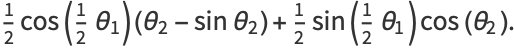 |
(11) |
Write (10) as
![A^_=1/(pi^2)[int_0^pisin(1/2theta_1)I_1dtheta_1+int_0^pisin(1/2theta_1)I_2dtheta_1],](http://mathworld.wolfram.com/images/equations/CircleTrianglePicking/NumberedEquation2.gif) |
(12) |
then
![I_1=int_(theta_1)^(2pi)sin(1/2theta_2)sin[1/2(theta_2-theta_1)]dtheta_2,](http://mathworld.wolfram.com/images/equations/CircleTrianglePicking/NumberedEquation3.gif) |
(13) |
and
![I_2=int_0^(theta_1)sin(1/2theta_2)sin[1/2(theta_1-theta_2)]dtheta_2.](http://mathworld.wolfram.com/images/equations/CircleTrianglePicking/NumberedEquation4.gif) |
(14) |
From (12),
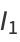 |
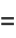 |
![1/2cos(1/2theta_2)[theta_2-sintheta_2]_(theta_1)^(2pi)+1/2sin(1/2theta_1)[costheta_2]_(theta_1)^(2pi)](http://mathworld.wolfram.com/images/equations/CircleTrianglePicking/Inline40.gif) |
(15) |
 |
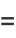 |
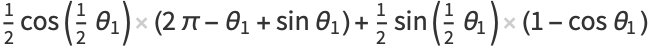 |
(16) |
 |
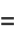 |
![picos(1/2theta_1)-1/2theta_1cos(1/2theta_1)+1/2[cos(1/2theta_1)sintheta_1-costheta_1sin(1/2theta_1)]+1/2sin(1/2theta_1)](http://mathworld.wolfram.com/images/equations/CircleTrianglePicking/Inline46.gif) |
(17) |
 |
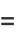 |
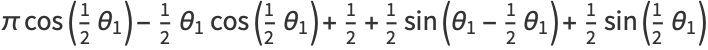 |
(18) |
 |
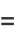 |
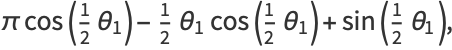 |
(19) |
so
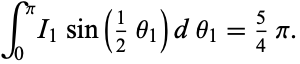 |
(20) |
Also,
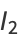 |
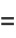 |
![1/2cos(1/2theta_1)[sintheta_2-theta_2]_0^(theta_1)-1/2sin(1/2theta_1)[costheta_2]_0^(theta_1)](http://mathworld.wolfram.com/images/equations/CircleTrianglePicking/Inline55.gif) |
(21) |
 |
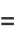 |
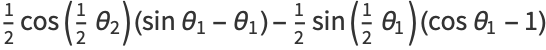 |
(22) |
 |
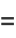 |
![-1/2theta_1cos(1/2theta_1)+1/2[sintheta_1cos(1/2theta_1)-costheta_1sin(1/2theta_2)]+1/2sin(1/2theta_1)](http://mathworld.wolfram.com/images/equations/CircleTrianglePicking/Inline61.gif) |
(23) |
 |
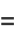 |
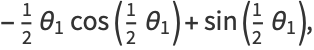 |
(24) |
so
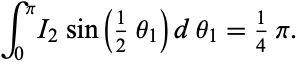 |
(25) |
Combining (◇) and (◇) gives the mean triangle area as
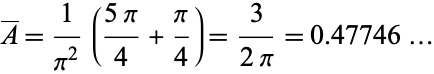 |
(26) |
(OEIS A093582).
The first few moments are
 |
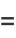 |
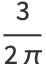 |
(27) |
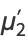 |
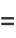 |
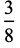 |
(28) |
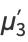 |
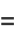 |
 |
(29) |
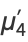 |
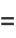 |
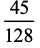 |
(30) |
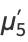 |
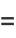 |
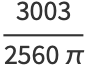 |
(31) |
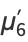 |
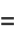 |
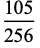 |
(32) |
(OEIS A093583 and A093584 and OEIS A093585 and A093586).
The variance is therefore given by
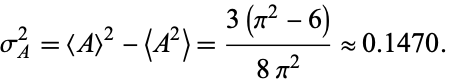 |
(33) |
The probability that the interior of the triangle determined by the three points picked at random on the circumference of a circle contains the origin is 1/4.
REFERENCES:
Sloane, N. J. A. Sequences A093582, A093583, A093584, A093585, and A093586 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|