


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-10-2019
Date: 1-2-2021
Date: 5-11-2020
|
Let 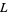 denote the
denote the 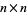 square lattice with wraparound. Call an orientation of
square lattice with wraparound. Call an orientation of 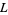 an assignment of a direction to each edge of
an assignment of a direction to each edge of 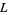 , and denote the number of orientations of
, and denote the number of orientations of 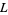 such that each vertex has two inwardly directed and two outwardly directly edges by
such that each vertex has two inwardly directed and two outwardly directly edges by 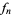 . Such an orientation is said to obey the ice rule, or to consist of Eulerian orientation. For
. Such an orientation is said to obey the ice rule, or to consist of Eulerian orientation. For 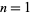 , 2, ..., the first few values of
, 2, ..., the first few values of 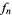 are 4, 18, 148, 2970, ... (OEIS A054759).
are 4, 18, 148, 2970, ... (OEIS A054759).
Lieb showed that
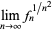 |
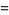 |
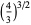 |
(1) |
 |
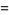 |
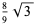 |
(2) |
 |
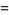 |
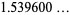 |
(3) |
(OEIS A118273; Finch 2003, p. 412), which is known as Lieb's square ice constant, also known as the square ice constant, residual entropy for square ice, and six-vertex entropy model.
REFERENCES:
Baxter, R. J. Exactly Solved Models in Statistical Mechanics. New York: Academic Press, 1982.
Bell, G. M. and Lavis, D. A. Statistical Methods of Lattice Systems, Vol. 1. New York: Springer-Verlag, 1999.
Bell, G. M. and Lavis, D. A. Statistical Methods of Lattice Systems, Vol. 2. New York: Springer-Verlag, 1999.
Finch, S. R. "Lieb's Square Ice Constant." §5.24 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 412-413, 2003.
Godsil, C.; Grötschel, M.; and Welch, D. J. A. "Combinatorics in Statistical Physics." In Handbook of Combinatorics, Vol. 2 (Ed. R. L. Graham, M. Grötschel, and L. Lovász). Cambridge, MA: MIT Press, pp. 1925-1954, 1995.
Lieb, E. H. "The Residual Entropy of Square Ice." Phys. Rev. 162, 162-172, 1967.
Lieb, E. H. "Exact Solution of the Problem of the Entropy of Two-Dimensional Ice." Phys. Rev. Lett. 18, 692-694, 1967.
Lieb, E. H. and Wu, F. Y. "Two-Dimensional Ferroelectric Models." In Phase Transitions and Critical Phenomena, Vol. 1 (Ed. C. Domb and M. S. Greene). New York: Academic Press, pp. 331-490, 1972.
Percus, J. K. Combinatorial Methods. New York: Springer-Verlag, 1971.
Sloane, N. J. A. Sequences A054759 and A118273 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|