
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-1-2020
Date: 31-10-2019
Date: 22-5-2020
|
Let ![R[z]>0](http://mathworld.wolfram.com/images/equations/IsekisFormula/Inline1.gif) ,
, 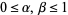 , and
, and
![Lambda(alpha,beta,z)=sum_(r=0)^infty[lambda((r+alpha)z-ibeta)+lambda((r+1-alpha)z+ibeta)],](http://mathworld.wolfram.com/images/equations/IsekisFormula/NumberedEquation1.gif) |
(1) |
where
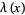 |
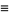 |
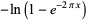 |
(2) |
 |
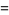 |
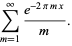 |
(3) |
Then if either 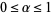 and
and 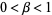 , or
, or 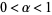 and
and 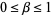 ,
,
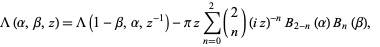 |
(4) |
where 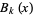 is a Bernoulli polynomial, and the second term on the right side can be written explicitly as
is a Bernoulli polynomial, and the second term on the right side can be written explicitly as
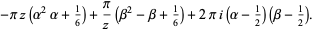 |
(5) |
REFERENCES:
Apostol, T. M. "Iseki's Transformation Formula" and "Deduction of Dedekind's Functional Equation from Iseki's Formula." §3.5-3.6 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 53-61, 1997.
Iseki, S. "The Transformation Formula for the Dedekind Modular Function and Related Functional Equations." Duke Math. J. 24, 653-662, 1957.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|