


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-9-2018
Date: 16-5-2018
Date: 25-5-2019
|
A zonal harmonic is a spherical harmonic of the form 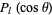 , i.e., one which reduces to a Legendre polynomial (Whittaker and Watson 1990, p. 302). These harmonics are termed "zonal" since the curves on a unit sphere (with center at the origin) on which
, i.e., one which reduces to a Legendre polynomial (Whittaker and Watson 1990, p. 302). These harmonics are termed "zonal" since the curves on a unit sphere (with center at the origin) on which 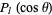 vanishes are
vanishes are 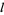 parallels of latitude which divide the surface into zones (Whittaker and Watson 1990, p. 392).
parallels of latitude which divide the surface into zones (Whittaker and Watson 1990, p. 392).
Resolving 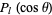 into factors linear in
into factors linear in 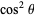 , multiplied by
, multiplied by 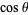 when
when 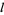 is odd, then replacing
is odd, then replacing 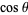 by
by 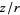 allows the zonal harmonic
allows the zonal harmonic 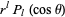 to be expressed as a product of factors linear in
to be expressed as a product of factors linear in 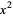 ,
, 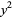 , and
, and 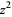 , with the product multiplied by
, with the product multiplied by 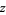 when
when 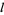 is odd (Whittaker and Watson 1990, p. 1990).
is odd (Whittaker and Watson 1990, p. 1990).
REFERENCES:
Byerly, W. E. "Zonal Harmonics." Ch. 5 in An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, pp. 144-194, 1959.
Hashiguchi, H. and Niki, N. "Algebraic Algorithm for Calculating Coefficients of Zonal Polynomials of Order Three." J. Japan. Soc. Comput. Statist. 10, 41-46, 1997.
Kowata, A. and Wada, R. "Zonal Polynomials on the Space of 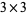 Positive Definite Symmetric Matrices." Hiroshima Math. J. 22, 433-443, 1992.
Positive Definite Symmetric Matrices." Hiroshima Math. J. 22, 433-443, 1992.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
مؤسسة السجناء السياسيين: سجلنا 120 ألفًا من ضحايا السجون والاعتقالات في عهد النظام السابق
|
|
|