Li's Criterion

Li's criterion states that the Riemann hypothesis is equivalent to the statement that, for

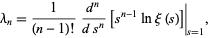(1)

where  is the xi-function,  for every positive integer  (Li 1997). Li's constants can be written in alternate form as

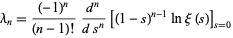(2)

(Coffey 2004).

 can also be written as a sum of nontrivial zeros  of  as

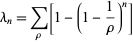(3)

(Li 1997, Coffey 2004).

A recurrence for 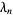 in terms of  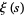is given by

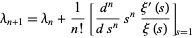(4)

(Coffey 2004).

The first few explicit values of the constantes 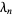 are

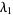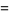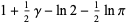			(5)
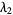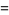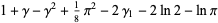			(6)
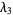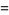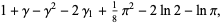			(7)

where  is the Euler-Mascheroni constant and  are Stieltjes constants. 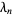 can be computed efficiently in closed form using recurrence formulas due to Coffey (2004), namely

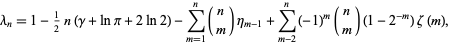(8)

where

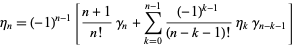(9)

and .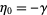

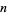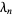		OEIS
1	0.0230957...	A074760
2	0.0923457...	A104539
3	0.2076389...	A104540
4	0.3687904...	A104541
6	0.5755427...	A104542
7	1.1244601...	A306340
8	1.4657556...	A306341

Edwards 2001 (p. 160) gave a numerical value for 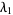, and numerical values to six digits up to  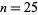were tabulated by Coffey (2004).

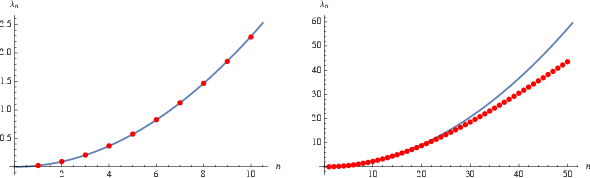
While the values of 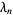 up to 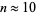 are remarkably well fit by a parabola with

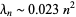(10)

(left figure above), larger terms show clear variation from a parabolic fit (right figure).

REFERENCES:

Bombieri, E. and Lagarias, J. C. "Complements to Li's Criterion for the Riemann Hypothesis." J. Number Th. 77, 274-287, 1999.

Coffey, M. W. "Relations and Positivity Results for Derivatives of the Riemann 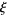 Function." J. Comput. Appl. Math. 166, 525-534, 2004.

Edwards, H. M. Riemann's Zeta Function. New York: Dover, 2001.

Keiper, J. B. "Power Series Expansions of Riemann's 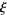 Function." Math. Comput. 58, 765-773, 1992.

Li, X.-J. "The Positivity of a Sequence of Numbers and the Riemann Hypothesis." J. Number Th. 65, 325-333, 1997.

Sloane, N. J. A. Sequences A074760, A104539, A104540, A104541, and A104542 in "The On-Line Encyclopedia of Integer Sequences."