


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-7-2019
Date: 2-5-2019
Date: 25-7-2019
|
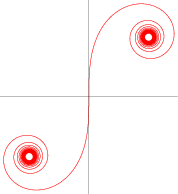
A plot in the complex plane of the points
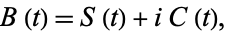 |
(1) |
where 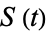 and
and 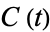 are the Fresnel integrals (von Seggern 2007, p. 210; Gray 1997, p. 65). The Cornu spiral is also known as the clothoid or Euler's spiral. It was probably first studied by Johann Bernoulli around 1696 (Bernoulli 1967, pp. 1084-1086). A Cornu spiral describes diffraction from the edge of a half-plane.
are the Fresnel integrals (von Seggern 2007, p. 210; Gray 1997, p. 65). The Cornu spiral is also known as the clothoid or Euler's spiral. It was probably first studied by Johann Bernoulli around 1696 (Bernoulli 1967, pp. 1084-1086). A Cornu spiral describes diffraction from the edge of a half-plane.
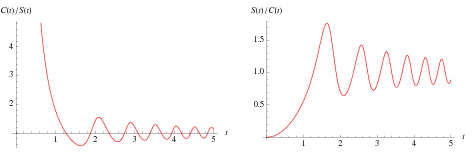
The quantities 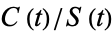 and
and 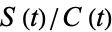 are plotted above.
are plotted above.
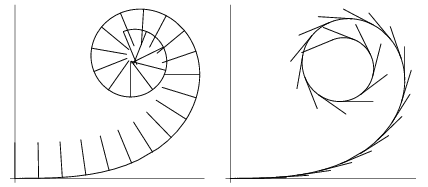
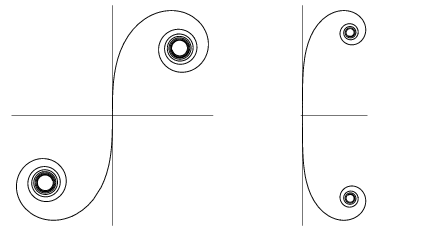
The slope of the curve's tangent vector (above right figure) is
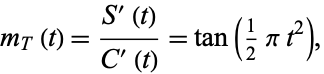 |
(2) |
plotted below.
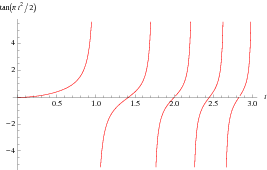
The Cesàro equation for a Cornu spiral is 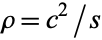 , where
, where 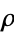 is the radius of curvature and
is the radius of curvature and  the arc length. The torsion is
the arc length. The torsion is 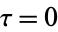 .
.
Gray (1997) defines a generalization of the Cornu spiral given by parametric equations
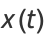 |
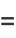 |
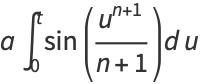 |
(3) |
 |
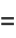 |
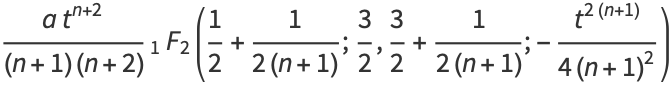 |
(4) |
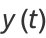 |
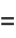 |
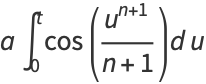 |
(5) |
 |
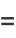 |
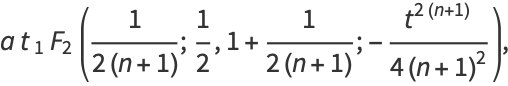 |
(6) |
where 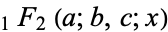 is a generalized hypergeometric function.
is a generalized hypergeometric function.
The arc length, curvature, and tangential angle of this curve are
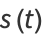 |
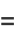 |
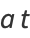 |
(7) |
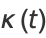 |
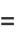 |
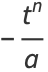 |
(8) |
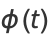 |
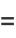 |
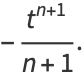 |
(9) |
The Cesàro equation is
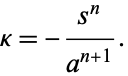 |
(10) |

Dillen (1990) describes a class of "polynomial spirals" for which the curvature is a polynomial function of the arc length. These spirals are a further generalization of the Cornu spiral. The curves plotted above correspond to 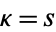 ,
, 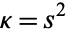 ,
, 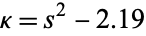 ,
, 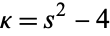 ,
, 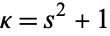 , and
, and 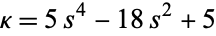 , respectively.
, respectively.
REFERENCES:
Bernoulli, J. Opera, Tomus Secundus. Brussels, Belgium: Culture er Civilisation, 1967.
Dillen, F. "The Classification of Hypersurfaces of a Euclidean Space with Parallel Higher Fundamental Form." Math. Z. 203, 635-643, 1990.
Gray, A. "Clothoids." §3.7 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 64-66, 1997.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 190-191, 1972.
von Seggern, D. CRC Standard Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 2007.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|