Legendre Function of the Second Kind

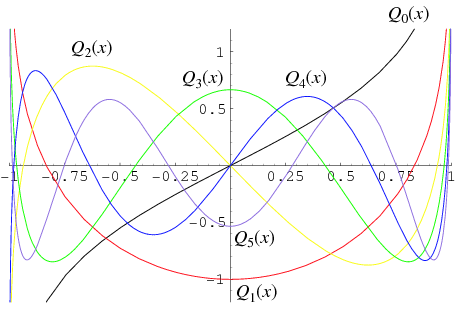
The second solution 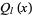 to the Legendre differential equation. The Legendre functions of the second kind satisfy the same recurrence relation as the Legendre polynomials. The Legendre functions of the second kind are implemented in the Wolfram Language as LegendreQ[l, x]. The first few are

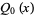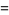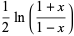			(1)
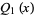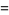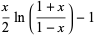			(2)
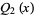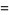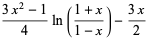			(3)
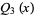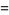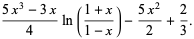			(4)

The associated Legendre functions of the second kind 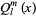 are the second solution to the associated Legendre differential equation, and are implemented in the Wolfram Language as LegendreQ[l, m, x]  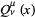has derivative about 0 of

(5)

(Abramowitz and Stegun 1972, p. 334). The logarithmic derivative is

(6)

(Binney and Tremaine 1987, p. 654).

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Legendre Functions." Ch. 8 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 331-339, 1972.

Arfken, G. "Legendre Functions of the Second Kind, 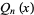." Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 701-707, 1985.

Binney, J. and Tremaine, S. "Associated Legendre Functions." Appendix 5 in Galactic Dynamics. Princeton, NJ: Princeton University Press, pp. 654-655, 1987.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 597-600, 1953.

Snow, C. Hypergeometric and Legendre Functions with Applications to Integral Equations of Potential Theory. Washington, DC: U. S. Government Printing Office, 1952.

Spanier, J. and Oldham, K. B. "The Legendre Functions 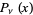 and 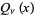." Ch. 59 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 581-597, 1987.