


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-7-2019
Date: 13-8-2018
Date: 15-9-2019
|
An algorithm which finds a polynomial recurrence for terminating hypergeometric identities of the form
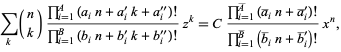 |
where 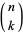 is a binomial coefficient,
is a binomial coefficient, 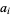 ,
, 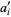 ,
, 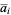 ,
, 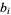 ,
, 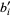 ,
, 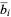 are constant integers and
are constant integers and 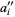 ,
, 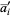 ,
, 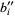 ,
, 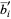 ,
, 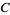 ,
,  , and
, and 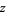 are complex numbers (Zeilberger 1990). The method was called creative telescoping by van der Poorten (1979), and led to the development of the amazing machinery of Wilf-Zeilberger pairs.
are complex numbers (Zeilberger 1990). The method was called creative telescoping by van der Poorten (1979), and led to the development of the amazing machinery of Wilf-Zeilberger pairs.
The also exists a 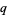 -analog of the algorithm, called the q-Zeilberger algorithm.
-analog of the algorithm, called the q-Zeilberger algorithm.
REFERENCES:
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.
Koepf, W. "Algorithms for 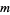 -fold Hypergeometric Summation." J. Symb. Comput. 20, 399-417, 1995.
-fold Hypergeometric Summation." J. Symb. Comput. 20, 399-417, 1995.
Koepf, W. "Zeilberger's Algorithm." Ch. 7 in Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, pp. 93-123, 1998.
Krattenthaler, C. "HYP and HYPQ: The Mathematica Package HYP." http://radon.mat.univie.ac.at/People/kratt/hyp_hypq/hyp.html.
Paule, P. "The Paule/Schorn Implementation of Gosper's and Zeilberger's Algorithms." http://www.risc.uni-linz.ac.at/research/combinat/risc/software/PauleSchorn/.
Paule, P. and Riese, A. "A Mathematica 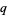 -Analogue of Zeilberger's Algorithm Based on an Algebraically Motivated Approach to
-Analogue of Zeilberger's Algorithm Based on an Algebraically Motivated Approach to 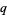 -Hypergeometric Telescoping." In Special Functions,
-Hypergeometric Telescoping." In Special Functions, 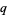 -Series and Related Topics, Fields Institute Communications 14, 179-210, 1997.
-Series and Related Topics, Fields Institute Communications 14, 179-210, 1997.
Paule, P. and Schorn, M. "A Mathematica Version of Zeilberger's Algorithm for Proving Binomial Coefficient Identities." J. Symb. Comput. 20, 673-698, 1995.
Petkovšek, M.; Wilf, H. S.; and Zeilberger, D. "Zeilberger's Algorithm." Ch. 6 in A=B. Wellesley, MA: A K Peters, pp. 101-119, 1996. http://www.cis.upenn.edu/~wilf/AeqB.html.
Riese, A. "A Generalization of Gosper's Algorithm to Bibasic Hypergeometric Summation." Electronic J. Combinatorics 1, No. 1, R19, 1-16, 1996. http://www.combinatorics.org/Volume_1/Abstracts/v1i1r19.html.
van der Poorten, A. "A Proof that Euler Missed... Apéry's Proof of the Irrationality of 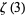 ." Math. Intel. 1, 196-203, 1979.
." Math. Intel. 1, 196-203, 1979.
Wegschaider, K. Computer Generated Proofs of Binomial Multi-Sum Identities. Diploma Thesis, RISC. Linz, Austria: J. Kepler University, May 1997. http://www.risc.uni-linz.ac.at/research/combinat/risc/software/MultiSum/.
Zeilberger, D. "Doron Zeilberger's Maple Packages and Programs: EKHAD." http://www.math.temple.edu/~zeilberg/programs.html.
Zeilberger, D. "A Fast Algorithm for Proving Terminating Hypergeometric Series Identities." Discrete Math. 80, 207-211, 1990.
Zeilberger, D. "A Holonomic Systems Approach to Special Function Identities." J. Comput. Appl. Math. 32, 321-368, 1990.
Zeilberger, D. "The Method of Creative Telescoping." J. Symb. Comput. 11, 195-204, 1991.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
ملاكات العتبة العباسية المقدسة تُنهي أعمال غسل حرم مرقد أبي الفضل العباس (عليه السلام) وفرشه
|
|
|