


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-9-2018
Date: 6-8-2019
Date: 19-5-2018
|
Kummer's first formula is
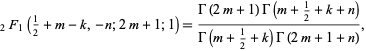 |
(1) |
where 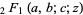 is the hypergeometric function with
is the hypergeometric function with 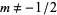 ,
, 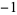 ,
, 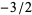 , ..., and
, ..., and 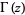 is the gamma function. The identity can be written in the more symmetrical form as
is the gamma function. The identity can be written in the more symmetrical form as
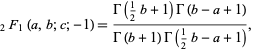 |
(2) |
where 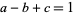 and
and 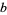 is a positive integer (Bailey 1935, p. 35; Petkovšek et al. 1996; Koepf 1998, p. 32; Hardy 1999, p. 106). If
is a positive integer (Bailey 1935, p. 35; Petkovšek et al. 1996; Koepf 1998, p. 32; Hardy 1999, p. 106). If 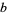 is a negative integer, the identity takes the form
is a negative integer, the identity takes the form
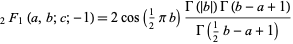 |
(3) |
(Petkovšek et al. 1996).
Kummer's second formula is
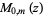 |
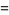 |
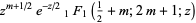 |
(4) |
 |
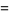 |
![z^(m+1/2)[1+sum_(k=1)^(infty)(z^(2k))/(2^(4k)k!(m+1)_k)]](http://mathworld.wolfram.com/images/equations/KummersFormulas/Inline14.gif) |
(5) |
 |
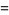 |
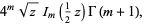 |
(6) |
where 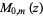 is a Whittaker function,
is a Whittaker function, 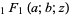 is the confluent hypergeometric function of the first kind,
is the confluent hypergeometric function of the first kind, 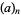 is a Pochhammer symbol,
is a Pochhammer symbol, 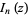 is a modified Bessel function of the first kind, and
is a modified Bessel function of the first kind, and 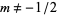 ,
, 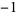 ,
, 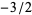 , ....
, ....
REFERENCES:
Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, 1935.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, 1998.
Petkovšek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A K Peters, pp. 42-43 and 126, 1996. http://www.cis.upenn.edu/~wilf/AeqB.html.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
هيأة المساءلة والعدالة: مؤتمر ذاكرة الألم يوثّق سنوات القهر التي عاشها العراقيون إبّان الحكم الجائر
|
|
|