


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-10-2019
Date: 19-9-2018
Date: 25-4-2018
|
The function defined by
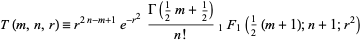 |
(1) |
(Heatley 1943; Abramowitz and Stegun 1972, p. 509), where 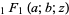 is a confluent hypergeometric function of the first kind and
is a confluent hypergeometric function of the first kind and 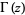 is the gamma function.
is the gamma function.
Heatley originally defined the function in terms of the integral
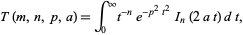 |
(2) |
where 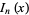 is a modified Bessel function of the first kind, which is similar to an integral of Watson (1966, p. 394), with Watson's
is a modified Bessel function of the first kind, which is similar to an integral of Watson (1966, p. 394), with Watson's 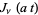 changed to
changed to 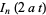 and a few other minor changes of variables. In terms of this function,
and a few other minor changes of variables. In terms of this function,
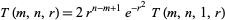 |
(3) |
(Heatley 1943). Heatley (1943) also gives a number of recurrences and other identities satisfied by 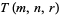 .
.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 509, 1972.
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 1. New York: Krieger, p. 268, 1981.
Heatley, A. H. "A Short Table of the Toronto Function." Trans. Roy. Soc. Canada 37, 13-29, 1943.
Slater, L. J. Confluent Hypergeometric Functions. Cambridge, England: Cambridge University Press, p. 99, 1960.
Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1966.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|