


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-5-2018
Date: 25-4-2019
Date: 19-9-2018
|
 |
Let 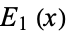 be the En-function with
be the En-function with 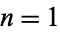 ,
,
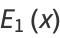 |
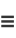 |
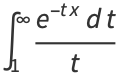 |
(1) |
 |
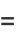 |
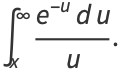 |
(2) |
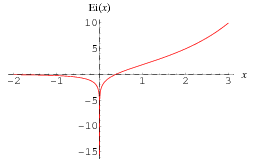
Then define the exponential integral 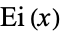 by
by
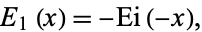 |
(3) |
where the retention of the 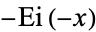 notation is a historical artifact. Then
notation is a historical artifact. Then 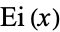 is given by the integral
is given by the integral
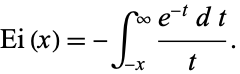 |
(4) |
This function is implemented in the Wolfram Language as ExpIntegralEi[x].
The exponential integral 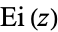 is closely related to the incomplete gamma function
is closely related to the incomplete gamma function 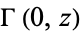 by
by
![Gamma(0,z)=-Ei(-z)+1/2[ln(-z)-ln(-1/z)]-lnz.](http://mathworld.wolfram.com/images/equations/ExponentialIntegral/NumberedEquation3.gif) |
(5) |
Therefore, for real 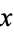 ,
,
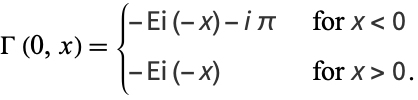 |
(6) |
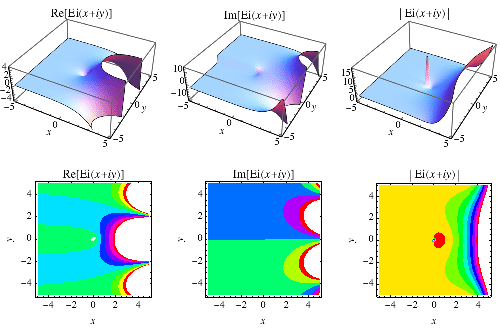
The exponential integral of a purely imaginary number can be written
![Ei(ix)=ci(x)+i[1/2pi+si(x)]](http://mathworld.wolfram.com/images/equations/ExponentialIntegral/NumberedEquation5.gif) |
(7) |
for 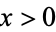 and where
and where 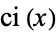 and
and 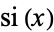 are cosine and sine integral.
are cosine and sine integral.
Special values include
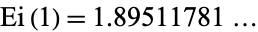 |
(8) |
(OEIS A091725).
The real root of the exponential integral occurs at 0.37250741078... (OEIS A091723), which is 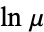 , where
, where 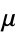 is Soldner's constant (Finch 2003).
is Soldner's constant (Finch 2003).
The quantity 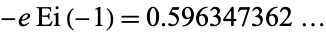 (OEIS A073003) is known as the Gompertz constant.
(OEIS A073003) is known as the Gompertz constant.
The limit of the following expression can be given analytically
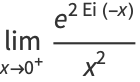 |
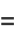 |
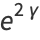 |
(9) |
 |
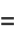 |
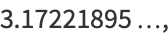 |
(10) |
(OEIS A091724), where 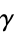 is the Euler-Mascheroni constant.
is the Euler-Mascheroni constant.
The Puiseux series of 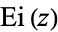 along the positive real axis is given by
along the positive real axis is given by
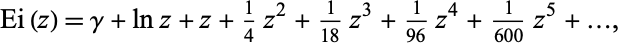 |
(11) |
where the denominators of the coefficients are given by 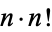 (OEIS A001563; van Heemert 1957, Mundfrom 1994).
(OEIS A001563; van Heemert 1957, Mundfrom 1994).
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 566-568, 1985.
Finch, S. R. "Euler-Gompertz Constant." §6.2 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 423-428, 2003.
Harris, F. E. "Spherical Bessel Expansions of Sine, Cosine, and Exponential Integrals." Appl. Numer. Math. 34, 95-98, 2000.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 105-106, 2003.
Jeffreys, H. and Jeffreys, B. S. "The Exponential and Related Integrals." §15.09 in Methods of Mathematical Physics, 3rd ed.Cambridge, England: Cambridge University Press, pp. 470-472, 1988.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 434-435, 1953.
Mundfrom, D. J. "A Problem in Permutations: The Game of 'Mousetrap.' " European J. Combin. 15, 555-560, 1994.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Exponential Integrals." §6.3 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 215-219, 1992.
Sloane, N. J. A. Sequences A001563/M3545, A073003, A091723, A091724, and A091725 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "The Exponential Integral Ei(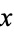 ) and Related Functions." Ch. 37 in An Atlas of Functions.Washington, DC: Hemisphere, pp. 351-360, 1987.
) and Related Functions." Ch. 37 in An Atlas of Functions.Washington, DC: Hemisphere, pp. 351-360, 1987.
van Heemert, A. "Cyclic Permutations with Sequences and Related Problems." J. reine angew. Math. 198, 56-72, 1957.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|