
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-4-2018
Date: 25-3-2019
Date: 25-4-2019
|
Let 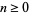 and
and 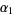 ,
, 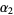 , ...be the positive roots of
, ...be the positive roots of 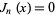 , where
, where 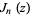 is a Bessel function of the first kind. An expansion of a function in the interval
is a Bessel function of the first kind. An expansion of a function in the interval 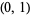 in terms of Bessel functions of the first kind
in terms of Bessel functions of the first kind
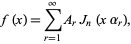 |
(1) |
has coefficients found as follows:
 |
(2) |
But orthogonality of Bessel function roots gives
![int_0^1xJ_n(xalpha_l)J_n(xalpha_r)dx=1/2delta_(l,r)[J_(n+1)(alpha_r)]^2](http://mathworld.wolfram.com/images/equations/Fourier-BesselSeries/NumberedEquation3.gif) |
(3) |
(Bowman 1958, p. 108), so
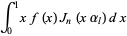 |
 |
![1/2sum_(r=1)^(infty)A_rdelta_(l,r)[J_(n+1)(alpha_r)]^2](http://mathworld.wolfram.com/images/equations/Fourier-BesselSeries/Inline9.gif) |
(4) |
 |
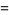 |
![1/2A_l[J_(n+1)(alpha_l)]^2,](http://mathworld.wolfram.com/images/equations/Fourier-BesselSeries/Inline12.gif) |
(5) |
and the coefficients are given by
![A_l=2/([J_(n+1)(alpha_l)]^2)int_0^1xf(x)J_n(xalpha_l)dx.](http://mathworld.wolfram.com/images/equations/Fourier-BesselSeries/NumberedEquation4.gif) |
(6) |
REFERENCES:
Bowman, F. Introduction to Bessel Functions. New York: Dover, 1958.
Kaplan, W. "Fourier-Bessel Series." §7.15 in Advanced Calculus, 4th ed. Reading, MA: Addison-Wesley, pp. 512-518, 1992.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|